(Diet problem) A dietician has to develop a special diet using two foods $P$ and $Q$ . Each packet (containing $30 g$ ) of food $P$ contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food $Q$ contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calciums atleast 460 units of iron and at most 300 units of cholesterol. How many packets of each food should be used to minimise the amount of vitamin A in the diet? What is the minimum amount of vitamin A? How many packets of each food should be used to maximise the amount of vitamin A in the diet? What is the maximum amount of vitamin A in the diet?

Video Solution

Text Solution

Verified by Experts

Let the dietician used $x$ packets of food $P$ and $y$ packets of food $Q$ . Then

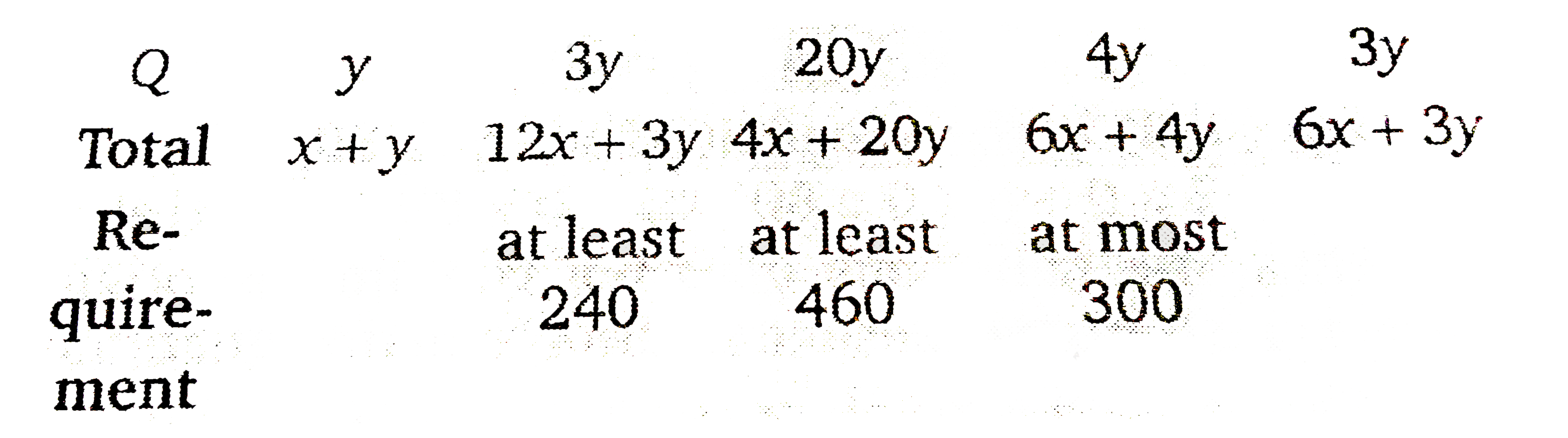
Minimise $Z = 6 x + 3 y$ …………………1
and constraints
$12 x + 3 y \geq 240 \Rightarrow 4 x + y \geq 80$ ………………2
$4 x + 2 y \geq 460 \Rightarrow x + 5 y \geq 115$ ……………….3
$6 x + 4 y \leq 300 \Rightarrow 3 x + 2 y \leq 150$ ..................4
$x \geq 0, y \geq 0$ ....................5
First draw the graph of the line $4 x + y = 80$ .

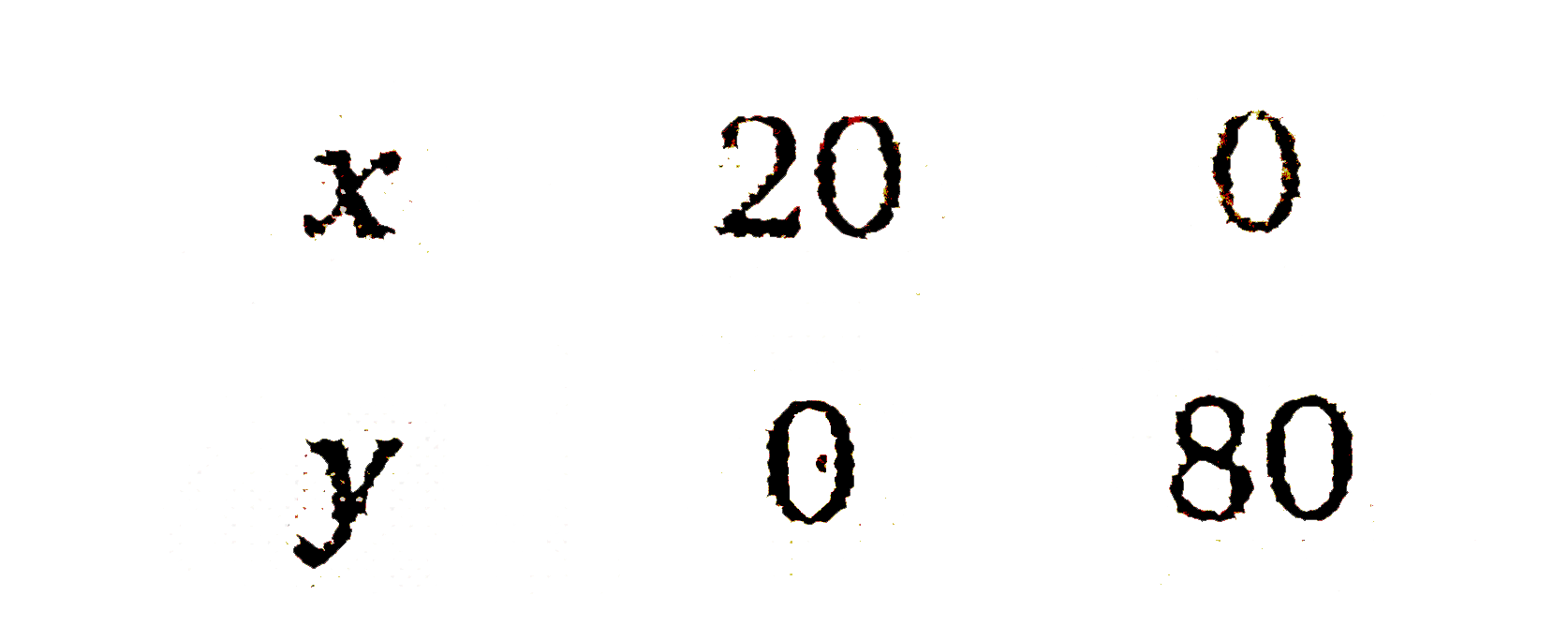
Put $(0, 0)$ in the inequation $4 x + y \geq 80$ ,
$4 \times 0 + 0 \geq 80 \Rightarrow 0 \geq 80$ (False)
Thus, the half plane does not contains origin.
Now, draw the graph of the line $x + 5 y = 115$

Put $(0, 0)$ in the equation $x + 5 y + 115$ ,
$0 + 5 \times 0 \geq 115 \Rightarrow 0 \geq 115$ (False)
Thus, the half plane does not contain the origin.
Now draw the graph of the line $3 x + 2 y = 150$

Put $(0, 0)$ in the inequation $3 x + 2 y \leq 150$
$3 \times 0 + 2 \times 0 \leq 150 \Rightarrow 0 \leq 150$ (True)
Therefore, half plane contains the origin. Since, $x, y \geq 0$ , so the feasible region lies in first quadrant.
From equations $4 x + y = 80$ and $x + 5 y = 115$ . The point of intersection is $A (15, 20)$ .
Similarly from equations $3 x + 2 y = 150$ and $x + 5 y = 115$ the point of intersection is $B (40, 15)$ . Thus the feasible region is ABCA.
Its vertices are $A (15, 20), B (40, 15)$ and $C (2, 72)$
We find the value of $Z$ at these vertices.

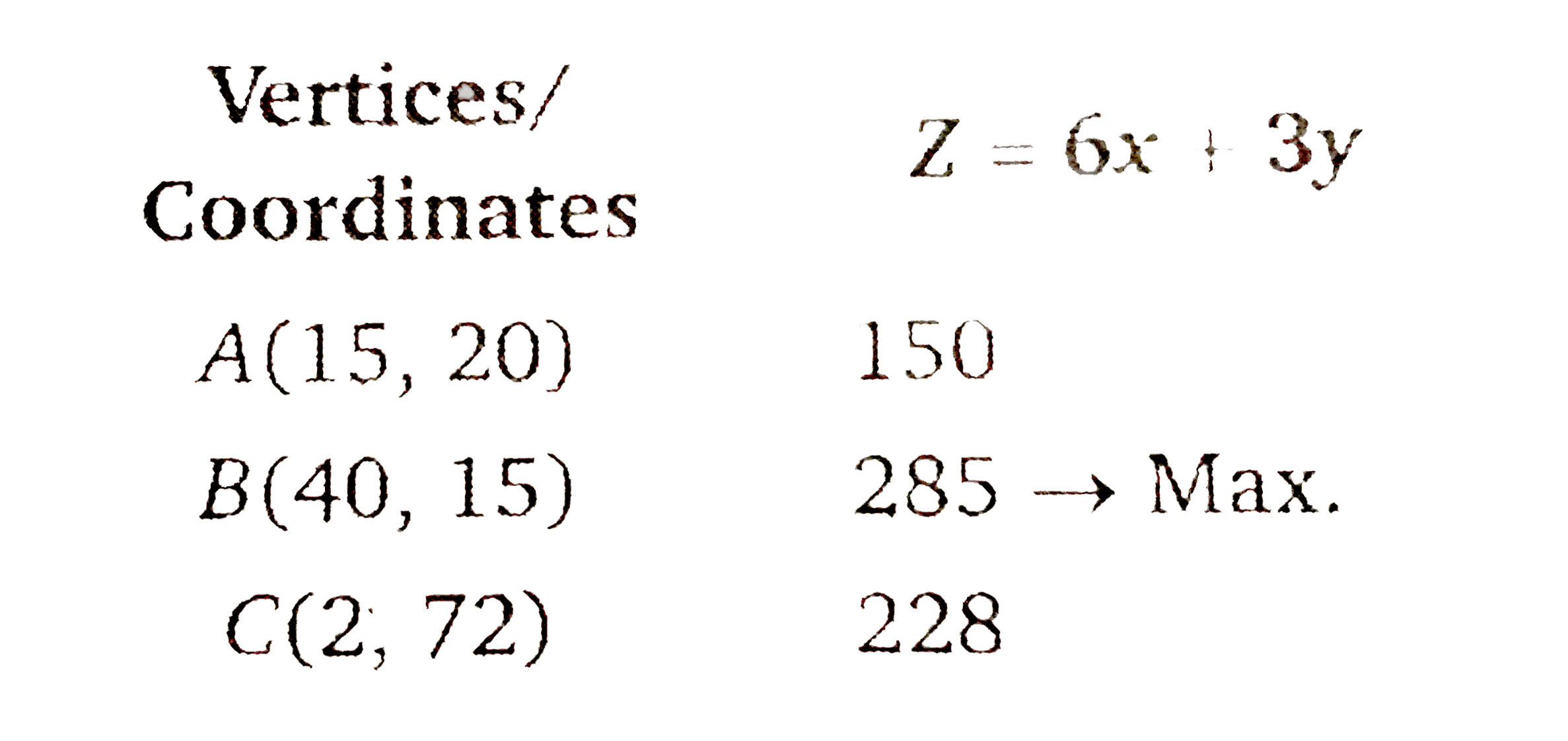
Thus, the maximum value of $Z$ is 285 at point $B (40, 15)$ . Therefore, to obtain the maximum vitamin A, 40 packages of food $P$ and 15 packages of food $Q$ should be produced. THus the maximum quantity of vitamin $A$ is 285.

Updated on:21/07/2023

Structural unit of vitamin-A is
A
B
C
D
Food X contains 4 units of vitamin A per gram and 7 units of vitamin B per gram and cost 15 paise per gram . Food Y contains 6 units of vitamin A per gram and 11 units of vitamin B per gram and cost 22 paise per gram . The daily minimum requirement of vitamin A and B are 90 units and 130 units respectively . The formulation of LPP to minimize the cost is
Az = 15x +22y, subject to constraints $4 x + 6 y \geq 90, 7 x + 11 y \geq 130, x \geq 0 y \geq 0$
Bz = 6x +5y, subject to constraints $4 x + 3 y \geq 90, 7 x + 11 y \geq 130, x \geq 0 y \geq 0$
Cz = 15x +62y, subject to constraints $4 x + 6 y \geq 90, 7 x + 11 y \geq 450, x \geq 0 y \geq 0$
Dz = 15x +22y, subject to constraints $4 x + 6 y \geq 90, 7 x + 45 y \geq 260, x \geq 0 y \geq 0$
Funtion units of food absorption are
AVilli
BBrunner's glands
CCrypts of Lieberkuhn
DPeyer's patches