Sketch the origin in which the points satisfying the following inequalities lie.
(i)|x+y|<2 (ii) |2x−y|>3 (iii) |x|>|y|
(i)|x+y|<2
∴−2<x+y<2
⇒x+y+2>0andx+y−2<0
L1(x,y)=x+y+2 and L2(x,y)=x+y−2
L1(0,0)=2>0 andL2(0,0)=−2<0
So ,x+y+2>0 represents the region where origin lies and x+y−2<0 also represents the region where origin lies.
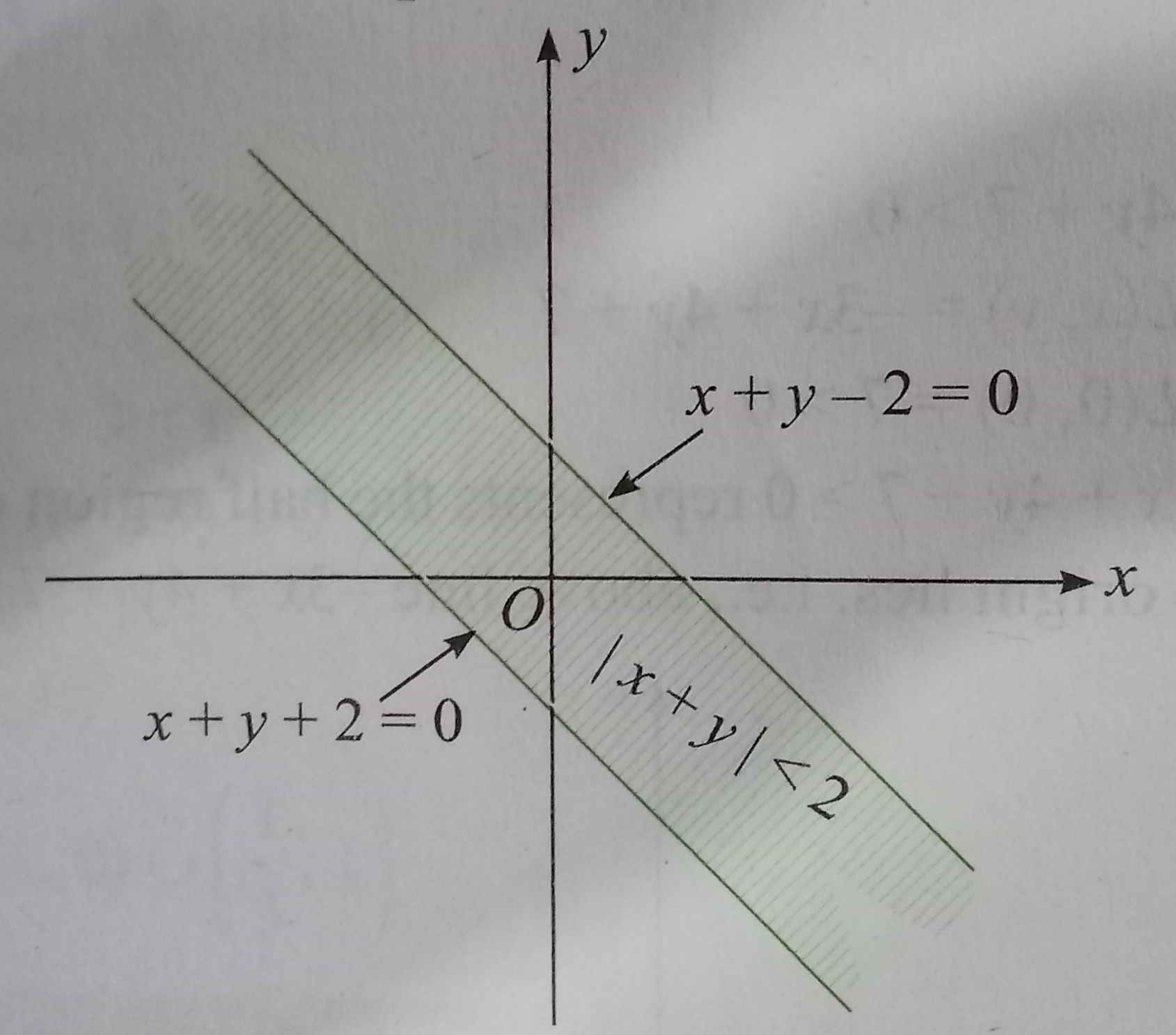
Thus, in general, |ax+by+c|<d is the region of the points
between the lines ax+by+c =d and ax+by+c = -d.
(ii)|2x−y|>3
∴2x−y<−3 and 2x−y>3
⇒2x−y+3<0 and 2x−y−3>0
L1(x,y)=2x−y+3 and L2(x,y)=2x−y−3
L1(0,0)=1>0 and L2(0,0)=−3<0
So, 2x−y+3<0 represents where origin doest not lie and 2x−y−3>0 also represents the region where origin does not lie.
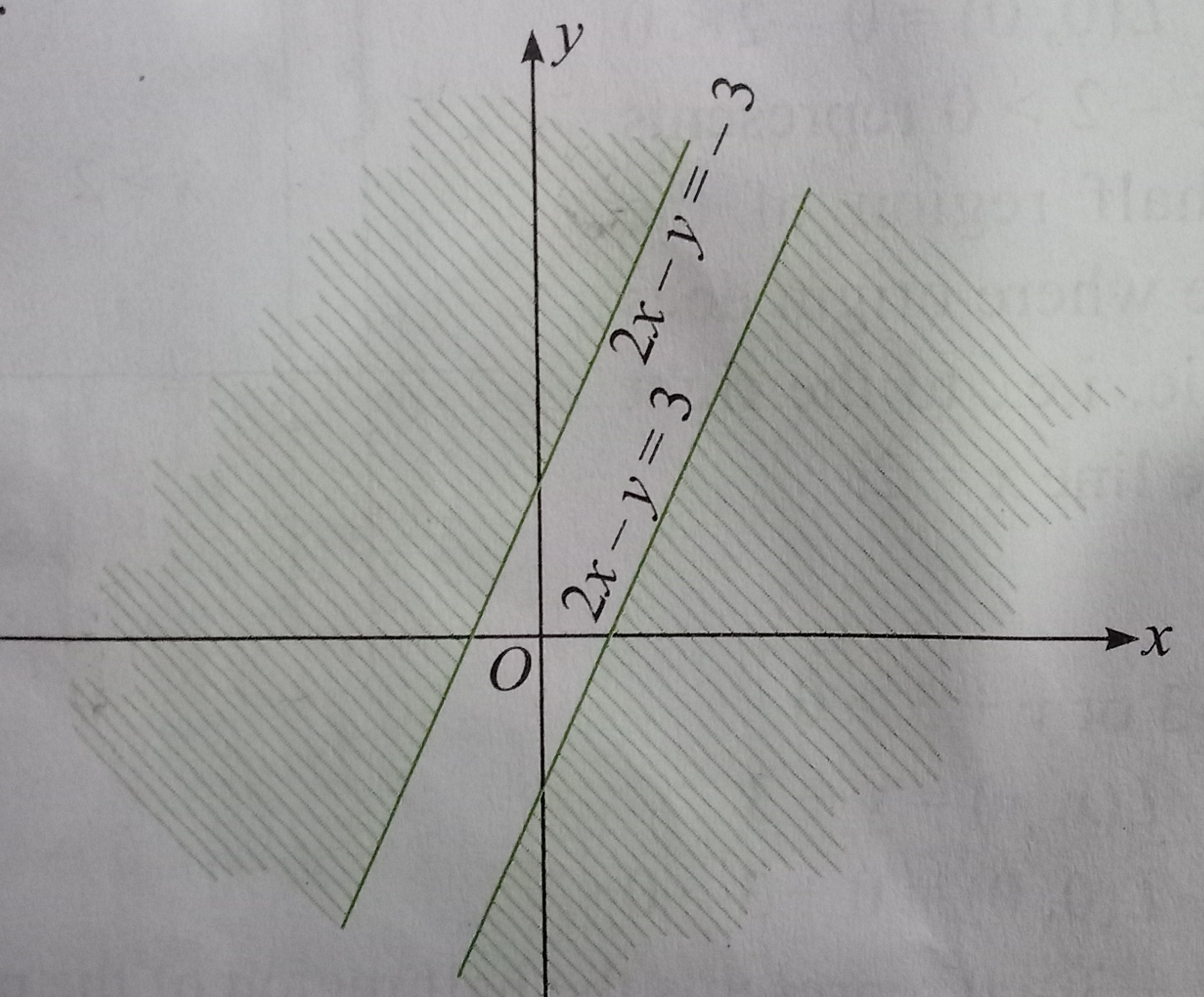
Thus, in general |ax+by+c|>d is the region of the points which does not lie between the lines ax+by+c =d and ax+by+c=-d.
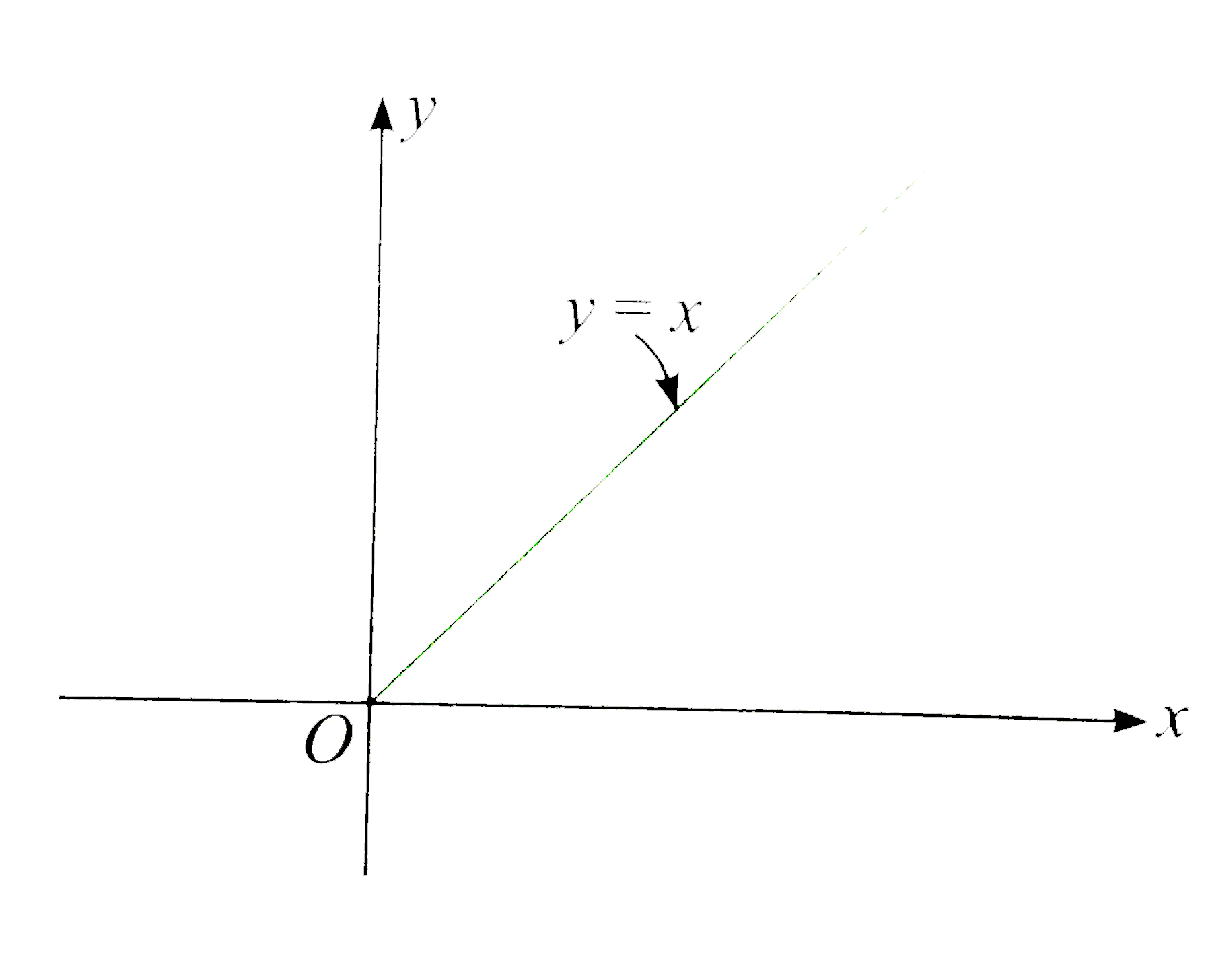
(iii)|x|>|y|
If x,y>0, then we have x>y orx−y>0.
Let L(x,y) = x-y.
∴L(1,0)=1−0>0.
Hence, points satisfying this inequality lie below the line x-y=0 in first quadrant.

Ifx>0,y>0, then we have x>−y orx+y>0.
Let L(x,y) = x+y.
∴L(1,0)=1+0>0
Points satisfying this inequality lie above the line x+y=0 in fourth quadrant.
Similarly, we have one region in second quadrant and one in third quadant.
Combining all the cases, we have following region.
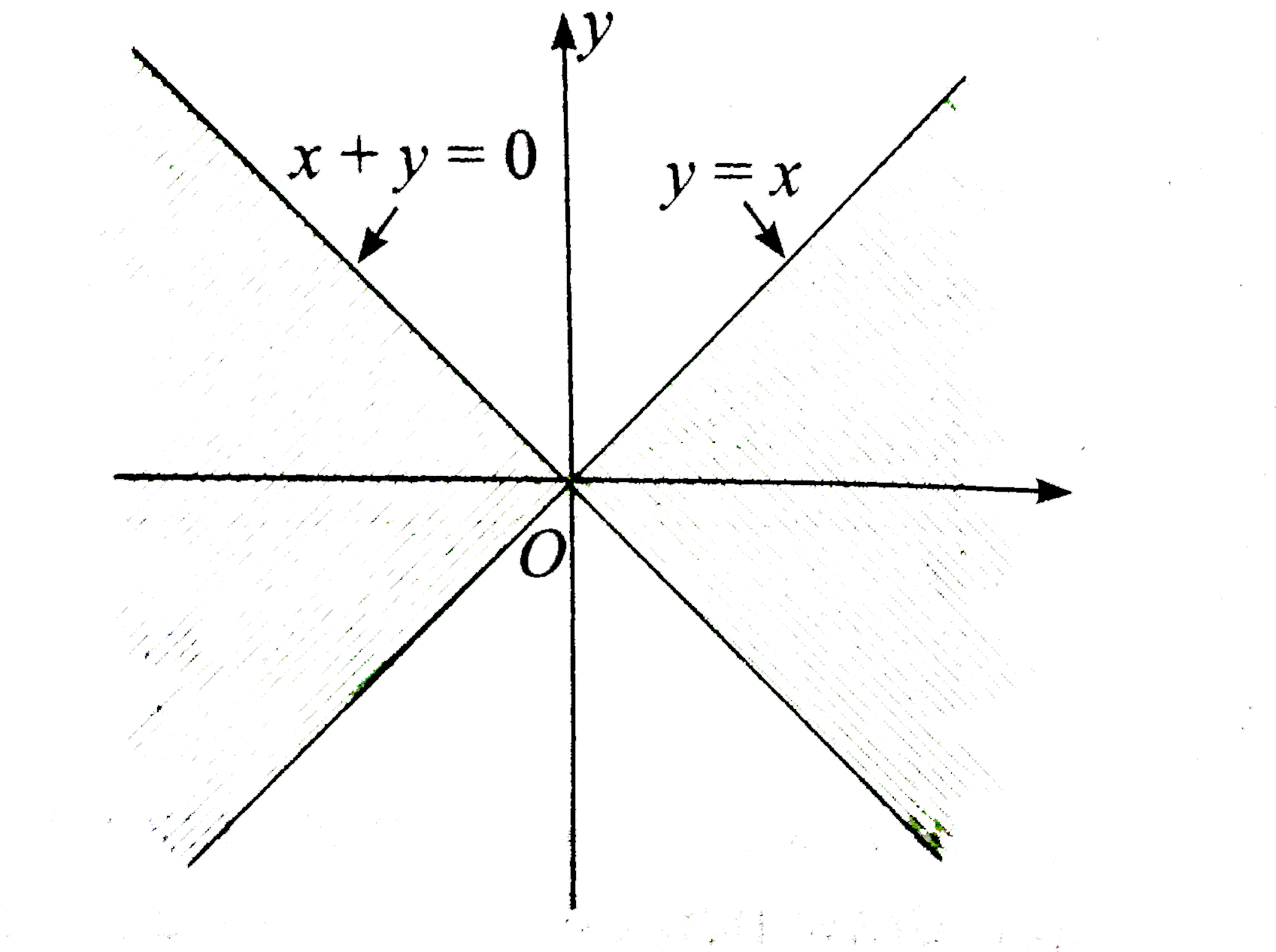
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Sketch the origin in which the points satisfying the following inequality lie.
(i)2x−3y−5>0 (ii) −3x+4y+7>0
(iii)x>2 (iv) y>−3
View SolutionSketch the origin in which the points satisfying the following inequality lie.
(i)2x−3y−5>0 (ii) −3x+4y+7>0
(iii)x>2 (iv) y>−3
View SolutionSketch the regions satisfying the following inequalities:
(a) x>2
(b) |y|≥1
View SolutionSketch the regions satisfying the following inequalities:
(a) x>2
(b) |y|≥1
View SolutionSketch the regions which points satisfy |x+y|≥2.
View SolutionSketch the regions which points satisfy |x+y|≥2.
View SolutionSolve the linear inequalities
2x−y>1,x−2y<1
View SolutionSolve the following inequations grapihically: (i)|x|≤3 (ii) |y−x|≤3
View SolutionProve the following inequalities :
tanx>x+x3/3if (0<x<π/2)
View SolutionSketch the region satisfying |x|<|y|.
View Solution
