Sketch the origin in which the points satisfying the following inequality lie.
(i)2x−3y−5>0 (ii) −3x+4y+7>0
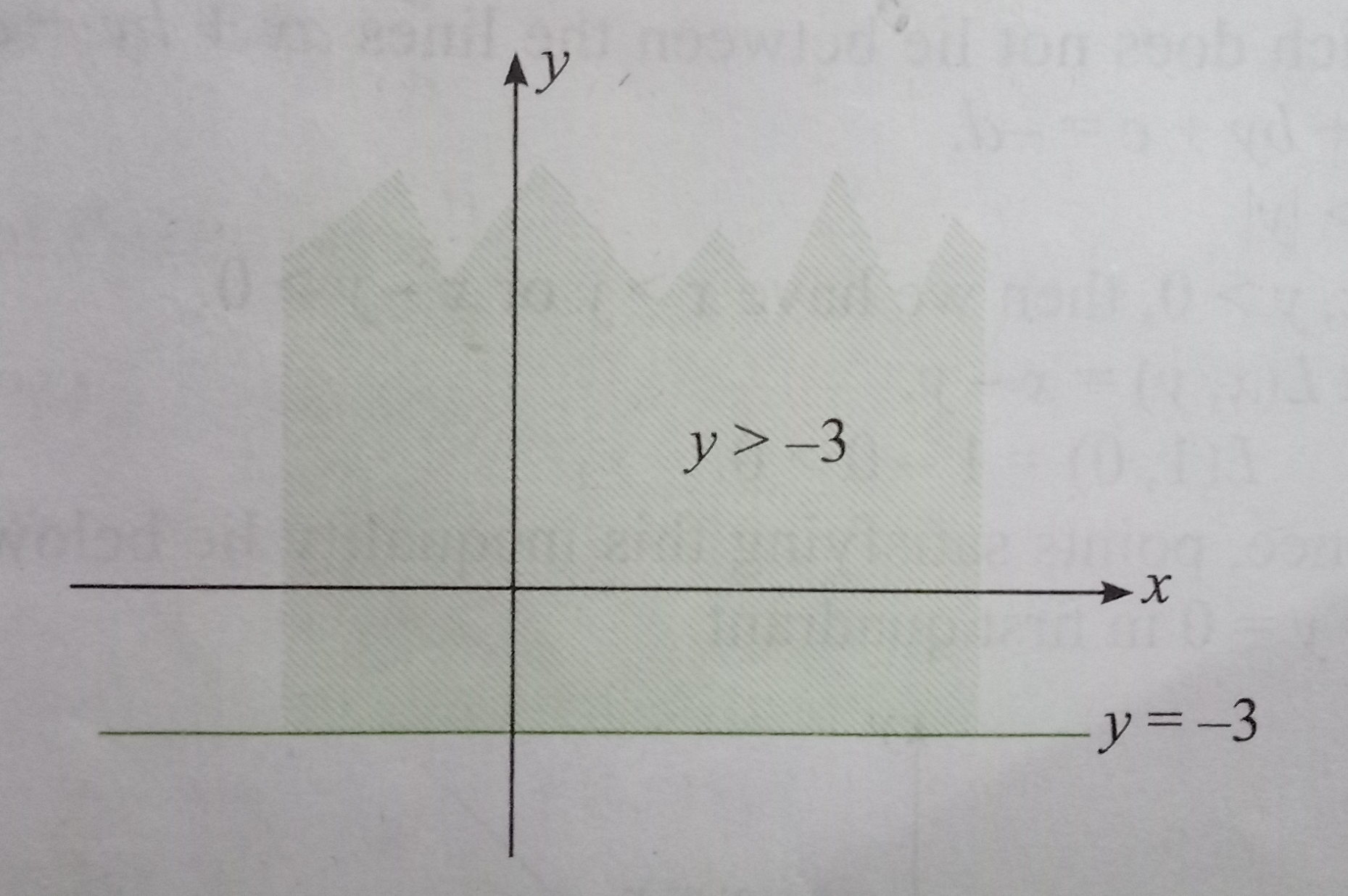
(iii)x>2 (iv) y>−3
Text Solution
(i)2x−3y−5>0
Let L(x,y)=2x−3y−5
L(0,0)=−5<0
So,2x−3y−5>0 represents the half origin of the plane where origin does not lie, i.e., below line 2x-3y-5=0.

(ii)−3x+4y+7>0
Let L(x,y) = -3x+4y+7
L(0,0)=7>0
SO, −3x+4y+7>0 represents the half region of the plane where origin lies, i.e., above line -3x+4y+7=0.


(iii)x>2orx−2>0
Let L(x,y) = x-2
L(0,0)=0−2<0
So, x−2>0 represents the half region of the plane where origin does not lie, i.e., the right of the line x=2.
(iv)y>−3ory+3>0
Let L(x,y) = y+3
L(0,0)=0+3>0
So,y+3>0 represents the half region of the plane where origin lies, i.e., above the line y+3=0.
|
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Knowledge Check
The ordered pairs (3,-1) satisfies which of the following inequalities?
I. x+3y>0
II. 2x+3y>2
III. x+y<0AI onlyBII onlyCI and III onlyDII and III onlyIs x−y>0 ?
I. x>y
II. x2>y2AIf statement (I) alone is sufficient to answer the question.BIf statement (II) alone is sufficient to answer the question.CIf either (I) or (II) alone is sufficient to answer the question.DIf both statements (I) and (II) taken together are sufficient to answer the question.Which of the following is a corner point of the feasible region of system of linear inequations 2x + 3y ≤6,x+4y≤4 and x, y ≥0 ?
A(1,0)B(1,1)C(0,3)D(125,25)
Sketch the regions satisfying the following inequalities:
(a) x>2
(b) |y|≥1
View SolutionSketch the regions satisfying the following inequalities:
(a) x>2
(b) |y|≥1
View SolutionSolve the following inequations
(i) x−3x−5>0
(ii) x+3x−2≤2.
View SolutionSolve the following inequations:
(i) 3x−6<0
(ii) −3x+9≤0
(iii) 7x+5>33
(iv) 5x−15≥0.
View SolutionFind the values that satisfy the polynomial inequation x4+4x3−12x2>0.
View Solution
