Solve dydx+yx=logx.Solution in Punjabi
Statement I is true, Statement II is also true , Statement II is the correct explanation of Statement I.
Statement I is true, Statement II is also true, Statement II is not the correct explanation of Statement I.
Statement I is true, Statement II is false.
Statement I is false, Statement II is true .
The correct Answer is:C
Step by step video & image solution for Solve (dy)/(dx)+(y)/(x)=log x. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Passage Based Questions)11videos
INDEFINITE INTEGRAL
- BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise 5 ( Matching Type Questions )2videos
INDEFINITE INTEGRAL
- BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (More Than One Correct Option Type Questions)5videos
INDEFINITE INTEGRAL
- BOOK - ARIHANT MATHSCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams3videos
HYPERBOLA
- BOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)8videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
If ∫f(x)cosxdx=12f2(x)+C, then f(x) can be
03:49View SolutionFind the mean marks of the following cummulative frequency table :
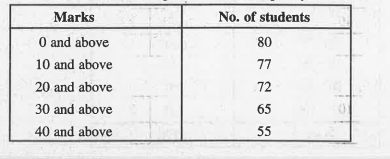
 04:22View Solution
04:22View SolutionFind: ∫dx(x+1)(x+2)
03:44View Solutionwhich term of the following sequence : 312,3,332.....is 81?
04:26View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
03:32View SolutionSolve x(dydx)=y(logy−logx+1)
03:34View SolutionSolve the equation dydx=y2y1ny+y−x
02:33View SolutionSolve x(dy)/(dx)+y=y^(2)ln x
02:38View Solutionअवकल समीकरण को हल कीजिए-
xdydx+y=xlogx01:50View SolutionSolve dydx+yx=logx.
05:19View Solutionहल कीजिए xlogxdy−ydx=0
03:32View SolutionSolvex log x(dy)/(dx) + y = 0
02:51View SolutionSolve y log y dx + (x-log y) dy = 0.
05:12View SolutionSolve: dydx=ex+y (ii) log(dydx)=ax+by
07:11View SolutionSolve the differential equation : x(dydx)+y=xlogx
06:01View SolutionSolve dydx+yx=logx.
06:30View Solution

