Solve the following inequation and write down the solution set:
11x−4<15x+4≤13x+14,x∈W .
The correct Answer is:Solution set = {0, 1, 2, 3, 4, 5}
To solve the given inequation 11x−4<15x+4≤13x+14 where x∈W (the set of whole numbers), we will break it down into two parts.
Step 1: Rewrite the Inequation
The given inequation is:
11x−4<15x+4≤13x+14
Step 2: Solve the Left Inequality
First, we will solve the left part of the inequality:
11x−4<15x+4
Subtract 11x from both sides:
−4<4x+4
Next, subtract 4 from both sides:
−4−4<4x
This simplifies to:
−8<4x
Now, divide both sides by 4:
−2<x
This can be rewritten as:
x>−2(Equation 1)
Step 3: Solve the Right Inequality
Now, we will solve the right part of the inequality:
15x+4≤13x+14
Subtract 13x from both sides:
2x+4≤14
Next, subtract 4 from both sides:
2x≤10
Now, divide both sides by 2:
x≤5(Equation 2)
Step 4: Combine the Results
Now we have two inequalities:
1. x>−2
2. x≤5
Step 5: Write the Solution Set
Combining these inequalities, we find:
−2<x≤5
Since x must be a whole number (as x∈W), the solution set in whole numbers is:
{0,1,2,3,4,5}
Final Answer
Thus, the solution set is:
{0,1,2,3,4,5}
The given inequation is:
11x−4<15x+4≤13x+14
First, we will solve the left part of the inequality:
11x−4<15x+4
Subtract 11x from both sides:
−4<4x+4
Next, subtract 4 from both sides:
−4−4<4x
This simplifies to:
−8<4x
Now, divide both sides by 4:
−2<x
This can be rewritten as:
x>−2(Equation 1)
Now, we will solve the right part of the inequality:
15x+4≤13x+14
Subtract 13x from both sides:
2x+4≤14
Next, subtract 4 from both sides:
2x≤10
Now, divide both sides by 2:
x≤5(Equation 2)
Now we have two inequalities:
1. x>−2
2. x≤5
Combining these inequalities, we find:
−2<x≤5
Since x must be a whole number (as x∈W), the solution set in whole numbers is:
{0,1,2,3,4,5}
Thus, the solution set is:
{0,1,2,3,4,5}
Topper's Solved these Questions
Similar Questions
Knowledge Check
The solution set of 11x−4<15x+4≤13x+14,x∈I, on the number line is
A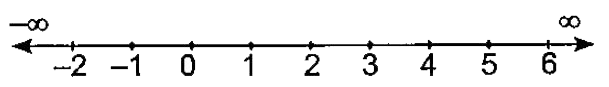 B
B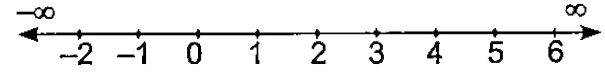 C
C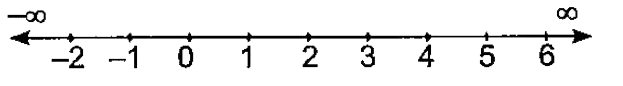 D
D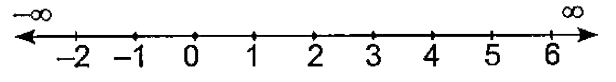
The solution set of −2+10x≤13x+10<24+10x,x∈Z is
A{−4,−3,−2,−1,0,1,2,3,4,5}B{−4,−3,−2,−1,0,1,2,3,4}C{−3,−2,−1,0,1,2,3,4}D{−3,−2,−1,0,1,2,3,4,5}
Solve the following inequation and graph the solution set on the number line :
2x−3<x+2≤3x+5,x∈R.
View SolutionSolve the inequation |4−x|+1<3
View SolutionSolve the following linear inequation: 2x−4≤0
View SolutionSolve the following inequation, write down the solution set and represent it on the real number line :
−2+10≤13x+10<24+10x,x∈Z
View SolutionSolve the following inequation and represent the solution set on the number line :
4x−19<3x5−2≤−25+x,∈R
View SolutionFor the following inequations, graph the solution set on the real number line :
−4≤3x−1<8
View Solution
