Somari sweeps 600 m long railway platform in 212 hours. His wife Imarati sweeps 23 rd of the same platform in 112 hours. Who sweeps more speedily?
Step by step video & image solution for Somari sweeps 600 m long railway platform in 2 1/2 hours. His wife Imarati sweeps 2/3\ r d of the same platform in 1 1/2\ hou r sdot Who sweeps more speedily? by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
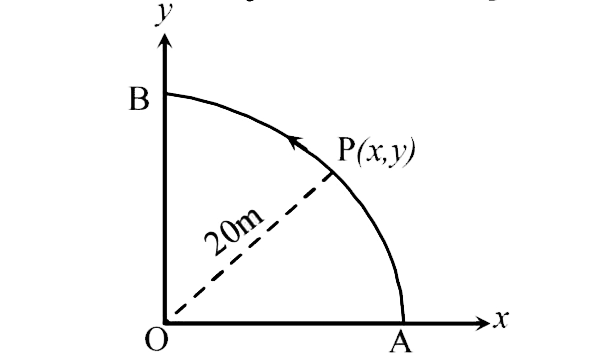
A point p moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length s=t3+5 , where s is in metres and t is in seconds . The radius of the path is 20m . The acceleration of 'P' when t=2s is nearly .
View SolutionX takes 3 hours more than Y to walk 30km. But, if X double his pace, he is ahead of Y by 112hours . Find their speed of walking.
View Solution
Knowledge Check
A man stands on a rotating platform with his arms stretched holding a 5kg weight in each hand. The angular speed of the platform is 1.2revs−1. The moment of inertia of the man together with the platform may be taken to be constant and equal to 6kgm2. If the man brings his arms close to his chest with the distance n each weight from the axis changing from 100cm to20cm. The new angular speed of the platform is.
A2revs−1B3revs−1C5revs−1D6revs−1A circular platform is mounted on a vertical frictionless axle. Its radius is r=2m and its moment of inertiaI=200kgm2. It is initially at rest. A 70kg man stands on the edge of the platform and begins to walk along the edge at speed v0=1ms−1 relative to the ground. The angular velocity of the platform is: a) 1.2 rad/s b) 0.4 rad/s c) 0.7 rad/s d) 2 rad/s
A1.2rads−1B0.4rads−1C0.7rads−1D2rads−1
Two blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between m1 and platform is 2μ and that between block m2 and platform is μ.The platform moves with an acceleration a . The normal reation between the blocks is

View SolutionA gun is fired from a moving platform and ranges of the shot are observed to be R1andR2 when the platform is moving forwards and backwards, respectively, with velocity vP. Find the elevation of the gun ∝ in terms of the given quantities.
View SolutionA platform is moving upwards with a constant acceleration of 2ms−2. At time t=0, a boy standing on the platform throws a ball upwards with a relative speed of 8ms−1. At this instant, platform was at the height of 4m from the ground and was moving with a speed of 2ms−1. Take g=0ms−2. Find
(a) when and where the ball strikes the platform.
(b) the maximum height attained by the ball from the ground.
( c) the maximum distance of the ball from the platform.
View SolutionA boy is sitting on a horizontal platform in the shape of a disc at a distance of 5m from its centre. The boy begins to slip when the speed of wheel exceeds 10 rpm. The coefficient of friction between the boy and platform is: (g=10ms−2)
View SolutionIn a double star system one of mass m1 and another of mass m2 with a separation d rotate about their common centre of mass. Then rate of sweeps of area of star of mass m1 to star of mass m2 about their common centre of mass is
View SolutionA square platform of side length 8m is is situated in x−z plane sucha that it is at 16m form the x-axis and 8m from the z-axis as shown in figure. A particle is projected with velocity →v=(v2^i+25ˆj)m/s relative to wind form origin and at the same instant the platform starts with acceleration →=(2ˆi+2.5ˆj)m/s2. Wind is blowing with velocity v1ˆk.g=10m/s2
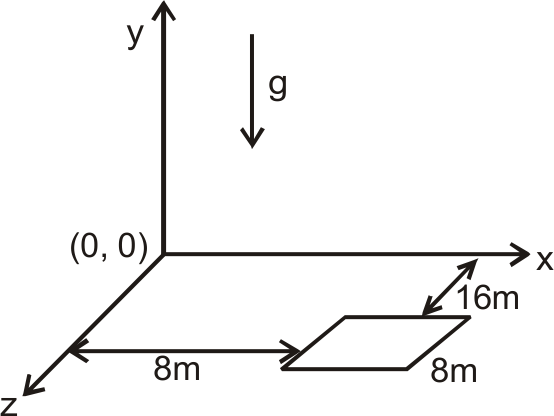
ListIList II(P)Least possible values of V2(in M/s) so that particle hits the platform or edge of platfrom is(1)4(Q)Least possible values of v1(in m/s) so that particle hits the platform or edge or platform is (2)6(Q)If t is the time (in seconds) after particle hits the platform then 2t is equal to (3)8(S)Value of displacement with respect to ground (in m) of the particle in y-direction , when v2 has its minimum possible value is (till particle hits the platform or edge of platform)(4)20
View Solution
