A platform is moving upwards with a constant acceleration of 2ms−2. At time t=0, a boy standing on the platform throws a ball upwards with a relative speed of 8ms−1. At this instant, platform was at the height of 4m from the ground and was moving with a speed of 2ms−1. Take g=0ms−2. Find
(a) when and where the ball strikes the platform.
(b) the maximum height attained by the ball from the ground.
( c) the maximum distance of the ball from the platform.
The correct Answer is:(a) 103s;
(b) 9 m
(c ) 83m.
To solve the problem step by step, let's break it down into parts (a), (b), and (c) as required.
Given Data:
- Acceleration of the platform, ap=2m/s2
- Initial velocity of the platform, up=2m/s
- Relative speed of the ball thrown upwards, ub=8m/s
- Initial height of the platform, hp=4m
- Acceleration due to gravity, g=0m/s2 (as per the question)
(a) When and where the ball strikes the platform
1. Calculate the actual initial velocity of the ball:
u=ub+up=8m/s+2m/s=10m/s
2. Calculate the relative acceleration of the ball with respect to the platform:
arelative=−g−ap=−0−2=−2m/s2
3. Use the equation of motion to find the time t when the ball strikes the platform:
The relative displacement srelative when the ball strikes the platform is 0:
srelative=ubt+12arelativet2=0
0=8t−12⋅2t2
0=8t−t2
t(t−8)=0
Thus, t=0 or t=8s.
4. Calculate the height of the platform when the ball strikes it:
Use the equation of motion for the platform:
h=hp+upt+12apt2
h=4+2⋅8+12⋅2⋅(82)
h=4+16+64=84m
(b) The maximum height attained by the ball from the ground
1. Use the equation of motion to find the maximum height:
At maximum height, the final velocity v=0:
v2=u2+2as
0=(10)2+2(−2)s
0=100−4s
4s=100⟹s=25m
2. Calculate the total maximum height from the ground:
Total height=hp+s=4+25=29m
(c) The maximum distance of the ball from the platform
1. Calculate the maximum distance of the ball from the platform:
The maximum distance occurs when the ball reaches its maximum height. The height of the platform at that time is:
hplatform=hp+upt+12apt2
where t=8s:
hplatform=4+2⋅8+12⋅2⋅(82)=84m
2. Calculate the maximum distance:
Distance=Maximum height of the ball−Height of the platform
Distance=29−84=−55m
This indicates that the ball is below the platform at its maximum height.
Summary of Results:
- (a) The ball strikes the platform at t=8s and at a height of 84m.
- (b) The maximum height attained by the ball from the ground is 29m.
- (c) The maximum distance of the ball from the platform is −55m (indicating the ball is below the platform).
- Acceleration of the platform, ap=2m/s2
- Initial velocity of the platform, up=2m/s
- Relative speed of the ball thrown upwards, ub=8m/s
- Initial height of the platform, hp=4m
- Acceleration due to gravity, g=0m/s2 (as per the question)
(a) When and where the ball strikes the platform
u=ub+up=8m/s+2m/s=10m/s
arelative=−g−ap=−0−2=−2m/s2
The relative displacement srelative when the ball strikes the platform is 0:
srelative=ubt+12arelativet2=0
0=8t−12⋅2t2
0=8t−t2
t(t−8)=0
Thus, t=0 or t=8s.
Use the equation of motion for the platform:
h=hp+upt+12apt2
h=4+2⋅8+12⋅2⋅(82)
h=4+16+64=84m
At maximum height, the final velocity v=0:
v2=u2+2as
0=(10)2+2(−2)s
0=100−4s
4s=100⟹s=25m
Total height=hp+s=4+25=29m
The maximum distance occurs when the ball reaches its maximum height. The height of the platform at that time is:
hplatform=hp+upt+12apt2
where t=8s:
hplatform=4+2⋅8+12⋅2⋅(82)=84m
Distance=Maximum height of the ball−Height of the platform
Distance=29−84=−55m
This indicates that the ball is below the platform at its maximum height.
- (a) The ball strikes the platform at t=8s and at a height of 84m.
- (b) The maximum height attained by the ball from the ground is 29m.
- (c) The maximum distance of the ball from the platform is −55m (indicating the ball is below the platform).
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Knowledge Check
A player throws a ball upwards with an initial speed of 30ms−1. How long does the ball take to return to the player's hands? ( Take g = 10 ms−2)
Aa. 3 sBb. 6 sCc. 9 sDd. 12 sA girl standing on a stationary lift (open from above) throws a ball upwards with initial speed 50ms−1. The time taken by the ball to return to her hands is (Take g = 10ms−2)
Aa. 5 sBb. 10 sCc. 15 sDd. 20 s
A balloon is moving along with constant upward acceleration of 1m/s2. A stone is thrown from the balloon downwards with speed 10m/s with respect to the balloon. At the time of projectile balloon is at height 120m from the ground and is moving with speed 20m/s. Find the time required to fall on the ground by the stone after the projection.
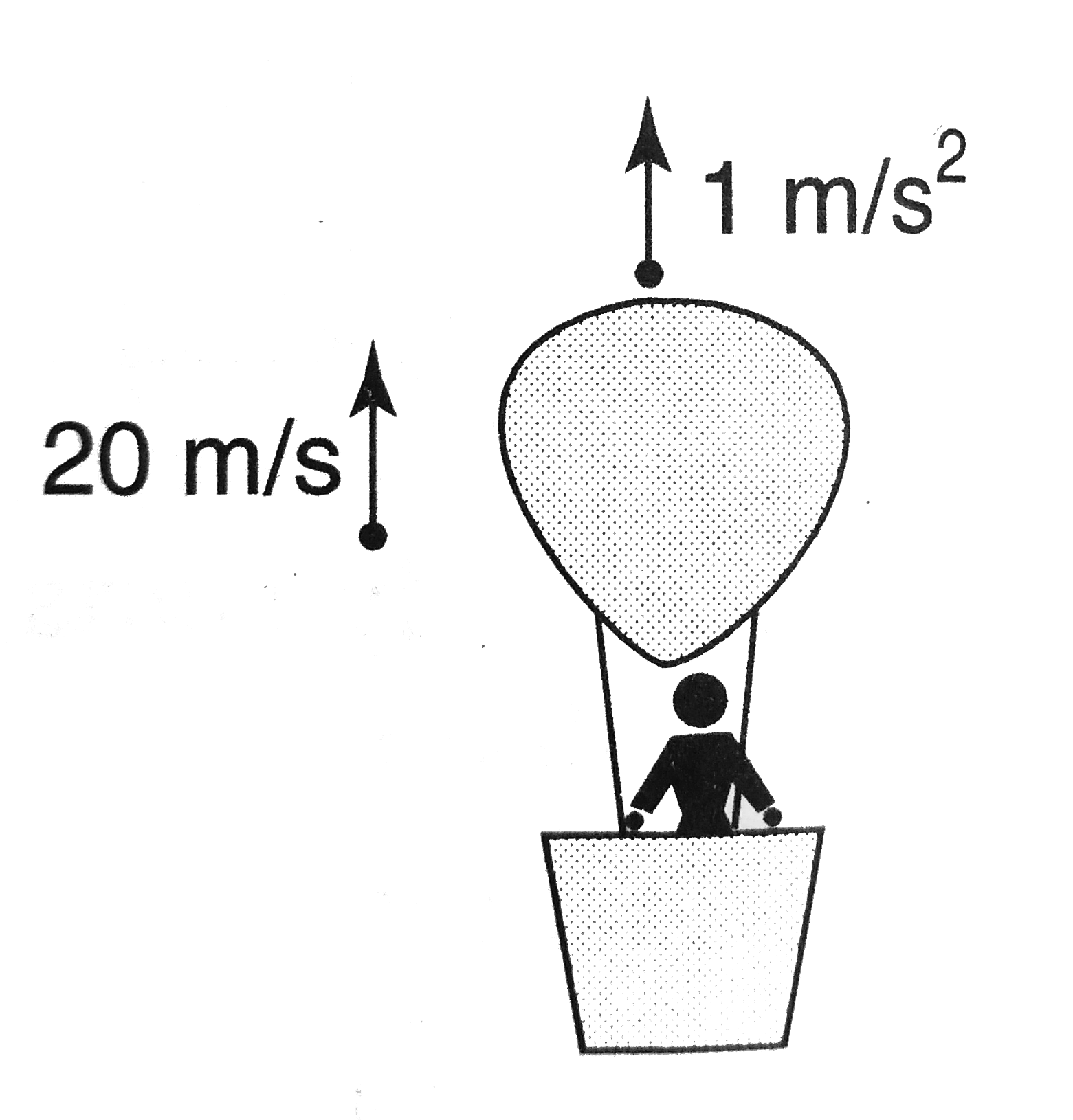
View SolutionA ball is thrown vertically upward from the 12 m level with an initial velocity of 18m/s. At the same instant an open platform elevator passes the 5 m level, moving upward with a constant velocity of 2m/s. Determine (g=9.8m/s2 )
(a) when and where the ball will meet the elevator,
(b) the relative velocity of the ball with respect to the elevator when the ball hits the elevator.
View SolutionA platform is moving upwards with an accelerations of 5ms−2. At the moment when its velocity is u=3ms−1, a ball is thrown from it with a speed of 30ms−1 w.r.t. platform at an angle of θ=30∘ with horizontal. The time taken by the ball to return to the platform is
View SolutionA pebble is thrown vertically upwards with a speed of 20 m s−1. How high will it be after 2 s? (Take g = 10 m s−2)
View SolutionA ball is projected vertically up with speed 20 m/s. Take g=10m/s2
View SolutionA train is moving along a straight line with a constant acceleration 'a' . A boy standing in the train throws a ball forward with a speed of 10m/s, at an angle of 60∘ to the horizontal. The boy has to move forward by 1.15m inside the train to catch the ball back at the initial height . the acceleration of the train , in m/s2 , is
View Solution
