A gun is fired from a moving platform and ranges of the shot are observed to be R1andR2 when the platform is moving forwards and backwards, respectively, with velocity vP. Find the elevation of the gun ∝ in terms of the given quantities.
The correct Answer is:tan−1[g4v2p×(R1−R2)2(R1+R2)].
To solve the problem, we need to analyze the motion of the projectile fired from a moving platform. Let's break it down step by step.
Step 1: Define the Variables
Let:
- u = initial horizontal component of the velocity of the projectile with respect to the platform.
- v = initial vertical component of the velocity of the projectile with respect to the platform.
- vP = velocity of the platform.
- R1 = range of the shot when the platform is moving forwards.
- R2 = range of the shot when the platform is moving backwards.
- g = acceleration due to gravity.
Step 2: Write the Range Equations
When the gun is fired from the moving platform:
1. For the forward motion:
R1=2(u+vP)vg
2. For the backward motion:
R2=2(u−vP)vg
Step 3: Add and Subtract the Range Equations
Now, we can add and subtract these two equations to eliminate u:
- Adding:
R1+R2=2(u+vP)vg+2(u−vP)vg
This simplifies to:
R1+R2=4uvg
- Subtracting:
R1−R2=2(u+vP)vg−2(u−vP)vg
This simplifies to:
R1−R2=4vPvg
Step 4: Square the Difference of Ranges
Now, we square the difference of the ranges:
(R1−R2)2=(4vPvg)2=16v2Pv2g2
Step 5: Express v in Terms of R1 and R2
From the previous equations, we can express v in terms of R1 and R2:
v2=g2(R1−R2)216v2P
Step 6: Substitute v into the Range Equation
Now, substitute v back into the equation for R1+R2:
R1+R2=4ug⋅
⎷g2(R1−R2)216v2P
This simplifies to:
R1+R2=4u(R1−R2)4vP⇒R1+R2=u(R1−R2)vP
Step 7: Solve for the Elevation Angle
The elevation angle α can be expressed as:
tanα=vu
Using the expressions derived earlier, we can substitute:
tanα=g4v2P⋅R1−R2R1+R2
Final Expression for Elevation
Thus, the elevation of the gun α is given by:
α=tan−1(g4v2P⋅R1−R2R1+R2)
Let:
- u = initial horizontal component of the velocity of the projectile with respect to the platform.
- v = initial vertical component of the velocity of the projectile with respect to the platform.
- vP = velocity of the platform.
- R1 = range of the shot when the platform is moving forwards.
- R2 = range of the shot when the platform is moving backwards.
- g = acceleration due to gravity.
When the gun is fired from the moving platform:
1. For the forward motion:
R1=2(u+vP)vg
2. For the backward motion:
R2=2(u−vP)vg
Now, we can add and subtract these two equations to eliminate u:
- Adding:
R1+R2=2(u+vP)vg+2(u−vP)vg
This simplifies to:
R1+R2=4uvg
R1−R2=2(u+vP)vg−2(u−vP)vg
This simplifies to:
R1−R2=4vPvg
Now, we square the difference of the ranges:
(R1−R2)2=(4vPvg)2=16v2Pv2g2
From the previous equations, we can express v in terms of R1 and R2:
v2=g2(R1−R2)216v2P
Now, substitute v back into the equation for R1+R2:
R1+R2=4ug⋅
⎷g2(R1−R2)216v2P
This simplifies to:
R1+R2=4u(R1−R2)4vP⇒R1+R2=u(R1−R2)vP
The elevation angle α can be expressed as:
tanα=vu
Using the expressions derived earlier, we can substitute:
tanα=g4v2P⋅R1−R2R1+R2
Thus, the elevation of the gun α is given by:
α=tan−1(g4v2P⋅R1−R2R1+R2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct76videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct11videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.411videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
Under isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
View SolutionA particle is thrown from a stationary platform with velocity v at an angle of 60∘ with the horizontal. The range obtained is R. If the platform moves horizontally in the direction of target with velocity v, the range will increase to :
View SolutionIf the range of a gun which fires a shell with muzzle speed V is R , then the angle of elevation of the gun is
View SolutionIf the range of a gun which fires a shell with muzzle speed V is R , then the angle of elevation of the gun is
View SolutionA planet of mass m moves around the Sun of mass Min an elliptical orbit. The maximum and minimum distance of the planet from the Sun are r1 and r2, respectively. Find the relation between the time period of the planet in terms of r1 and r2.
View SolutionA gun of mass M(including the carriage) fires a shot of mass m. The gun along with the carriage is kept on a smooth horizontal surface. The muzzle speed of the bullet vr is constant. Find
(a) The elevation of the gun with horizontal at which maximum range of bullet with respect to the ground is obtained.
(b) The maximum range of the bullet.View Solution
A particle is moving on a circular path of radius r with uniform velocity v. The change in velocity when the particle moves from P to Q is (∠POQ=40∘)View SolutionA man standing in front of a vertical cliff fires a gun. He hears the echo after 3 s. On moving closer to the cliff by 82-5 m, he fires again and hears the echo after 2.5 s. Find :
the distance of the cliff from the initial position of the man,View SolutionTwo particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
 .View Solution
.View SolutionA uniform disc of radius R rolls perfectly over two horizontal plank A and B moving with velocities v and 2v, spectively. Find the
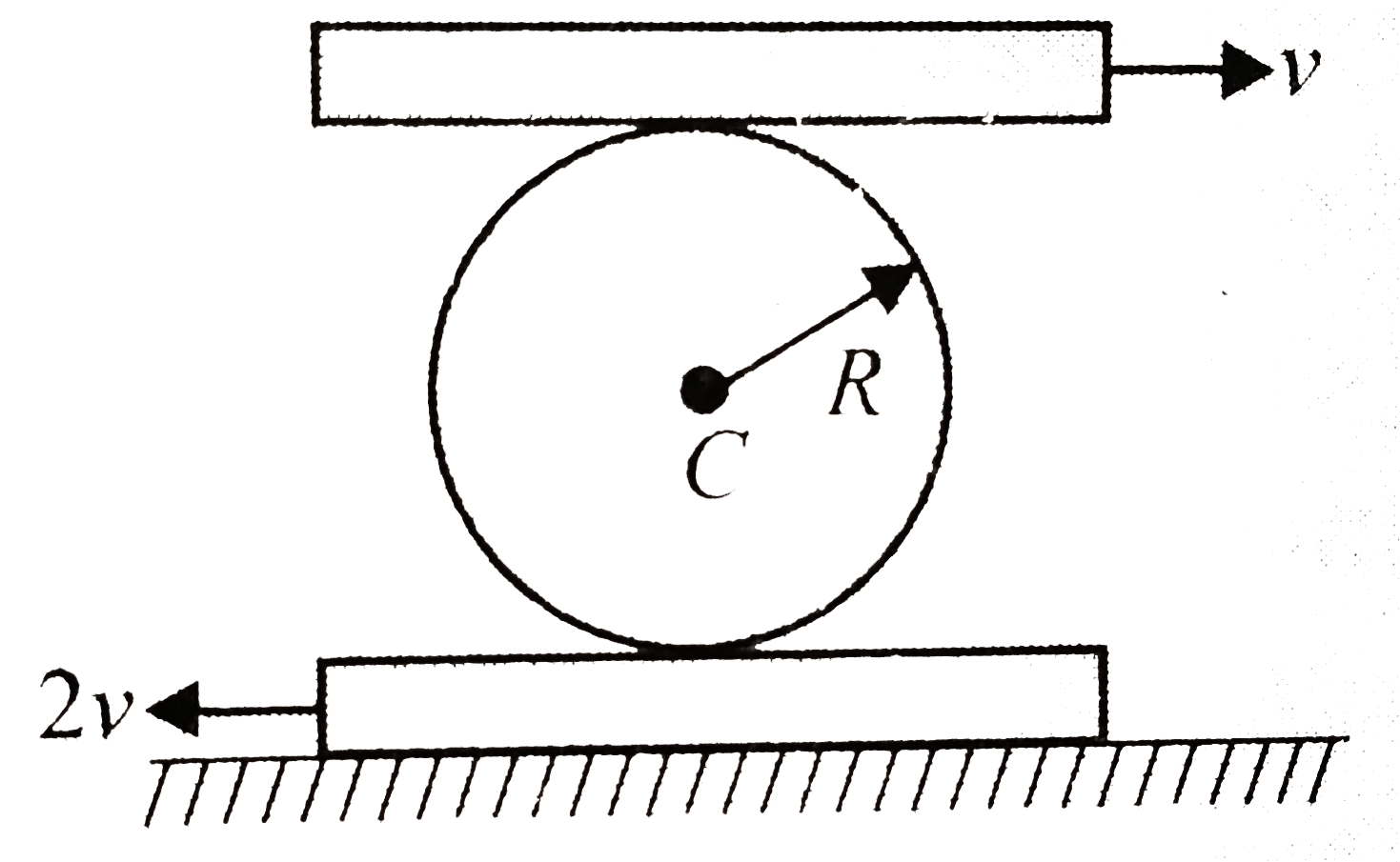
a. velocity of CM of the disc.
b. angular velocity of the disc.View Solution

