□ABCD is a parallelogram. Point E is on side BC. Line DE intersects ray AB in point T. Prove that DE×BE=CE×TE.
Step by step video & image solution for squareABCD is a parallelogram. Point E is on side BC. Line DE intersects ray AB in point T. Prove that DExxBE=CExxTE. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
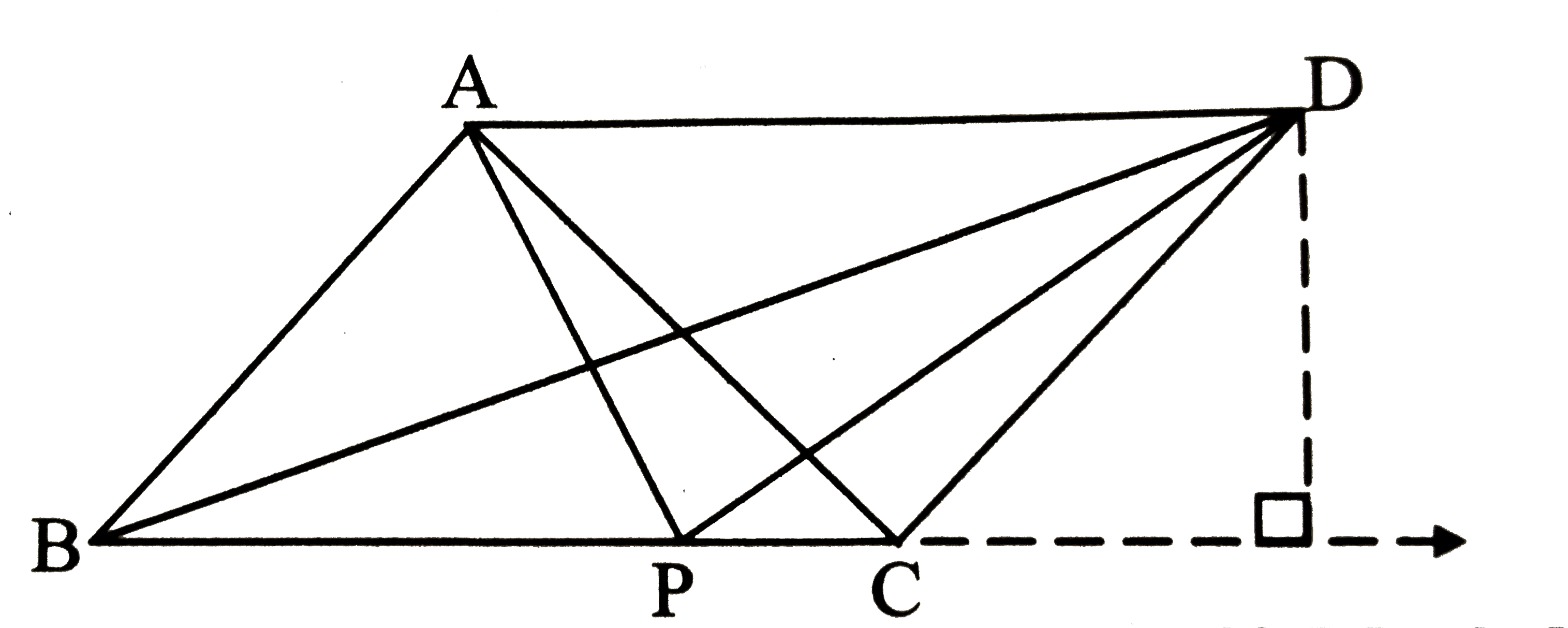
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC
□ABCD is a parallelogram. P is any point on side BC. Find two pairs of triangles with equal areas.
 View Solution
View SolutionIn the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.
 View Solution
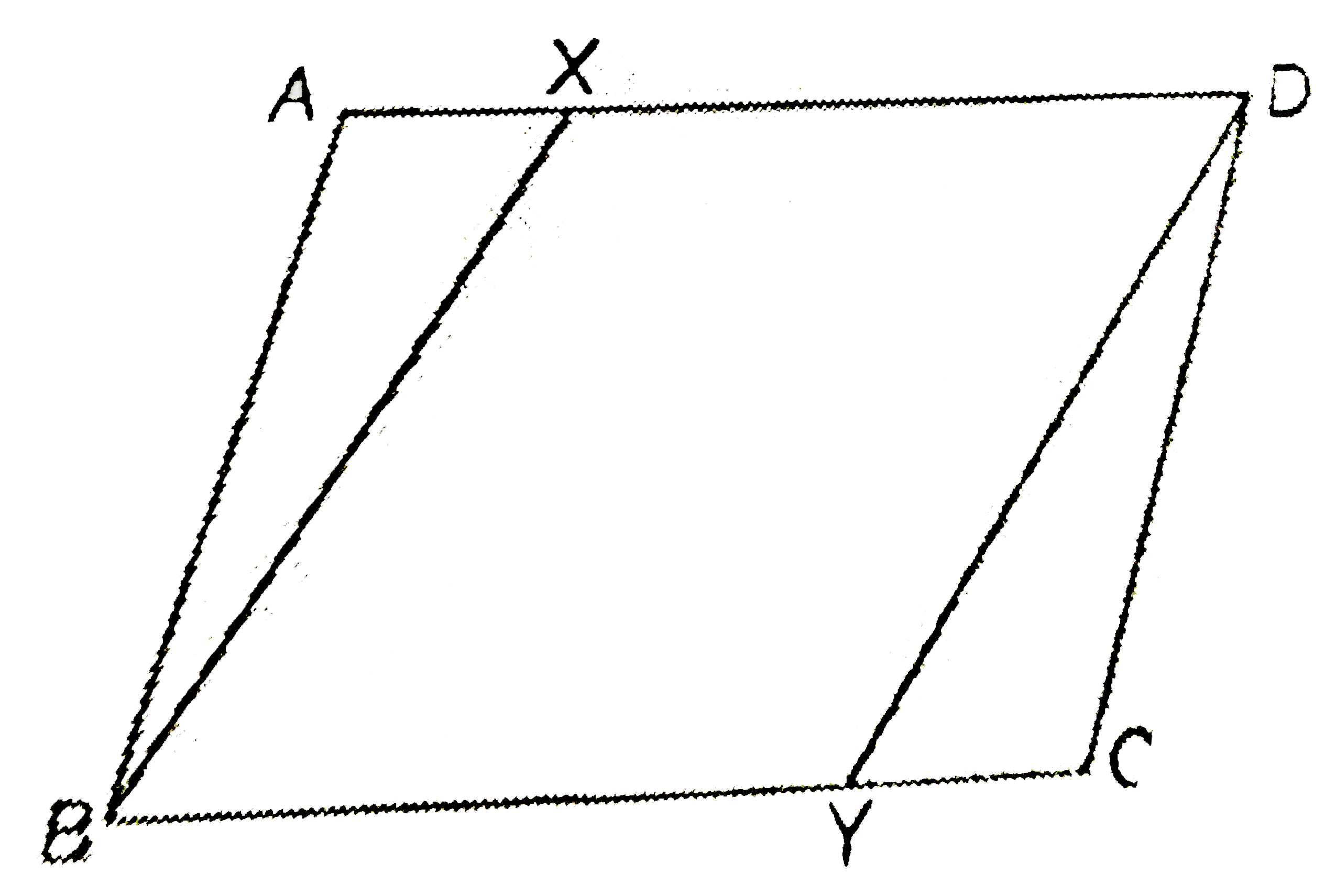
View SolutionIn the adjoining figure □ABCD is a parallelogeam. Points X and Y lie on the sides AD and BC respectively and AX=14ADandCY=14BC. Show that □XBYD is a parallelogram.
 View Solution
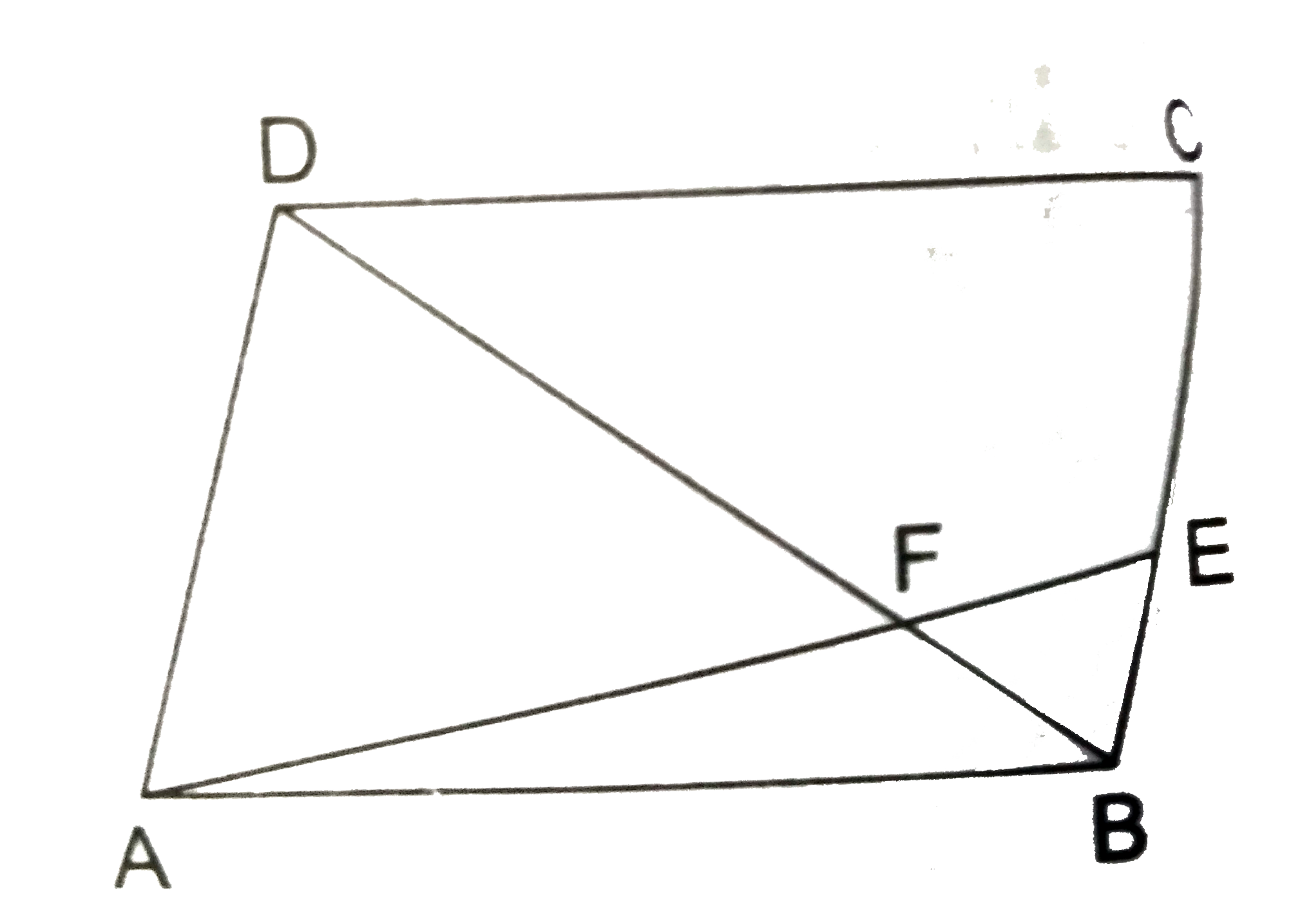
View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the Side BC. Prove that DF×EF=FB×FA.
View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC . Prove that DFxEF=FBxFA.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View SolutionIn rectangle ABCD, E is the midpoint of side BC. Prove that, AE = DE.
View Solution