State which of the following statements is true of false.
(i) If $x < y and b < 0, then \frac{x}{b} < \frac{y}{b}$ .
(ii) If $x y > 0, then x > 0 and y < 0$
(iii) If $x y > 0, then x < 0 and y < 0$
(iv) If $x y < 0, then x < 0 and y < 0$
(v) If $x < - 5 and x < - 2, than x \in (- \infty, - 5)$
(vi) If $x < - 5 and x > 2, then x \in (- 5, 2)$
(vii) If $x > - 2 and x < 9, then x \in (- 2, 9)$
(viii) If $| x | > 5, then x \in (- \infty, - 5) \cup [5, \infty)$
(ix) If $| x | \leq 4, then x \in [- 4, 4]$
(x) $Graph of x < 3$ is

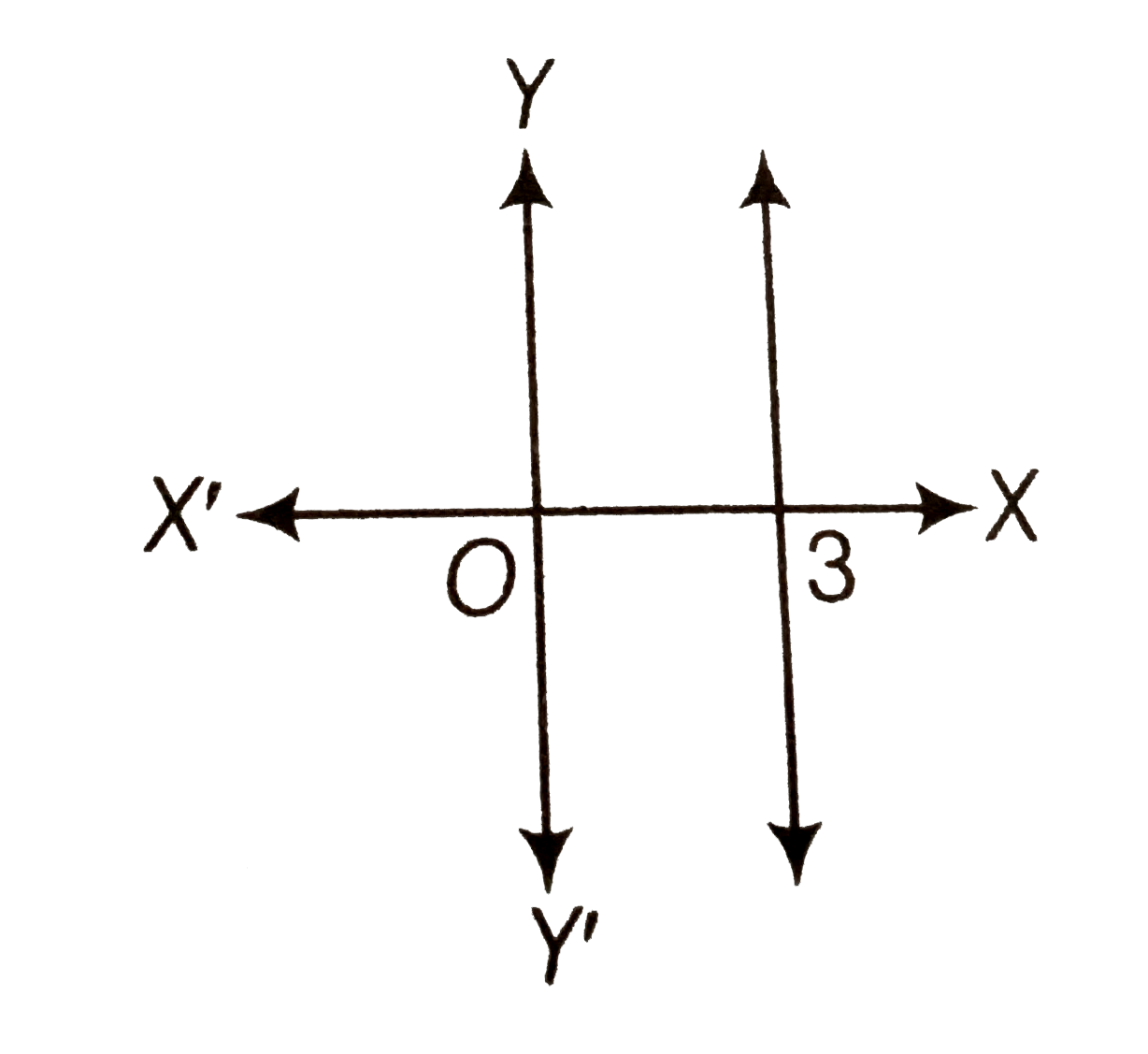
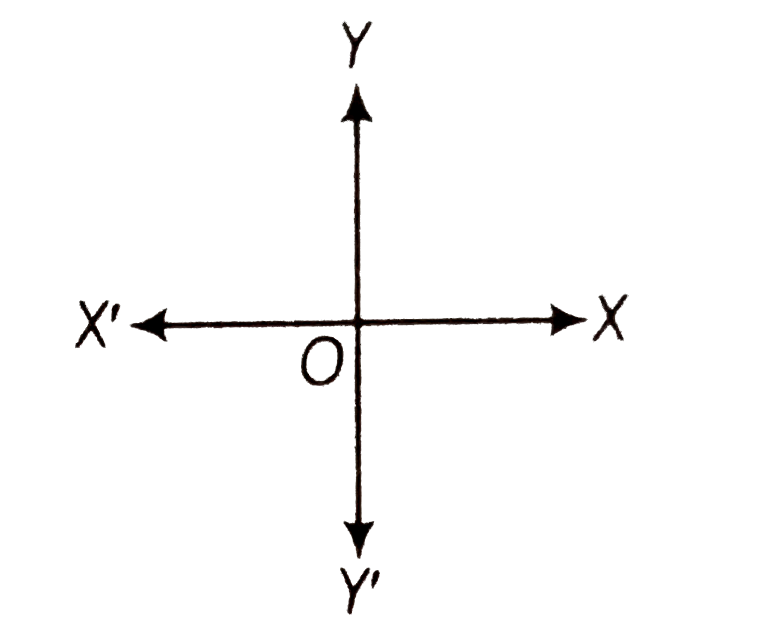
(xi) Graph of $x \geq 0$ is

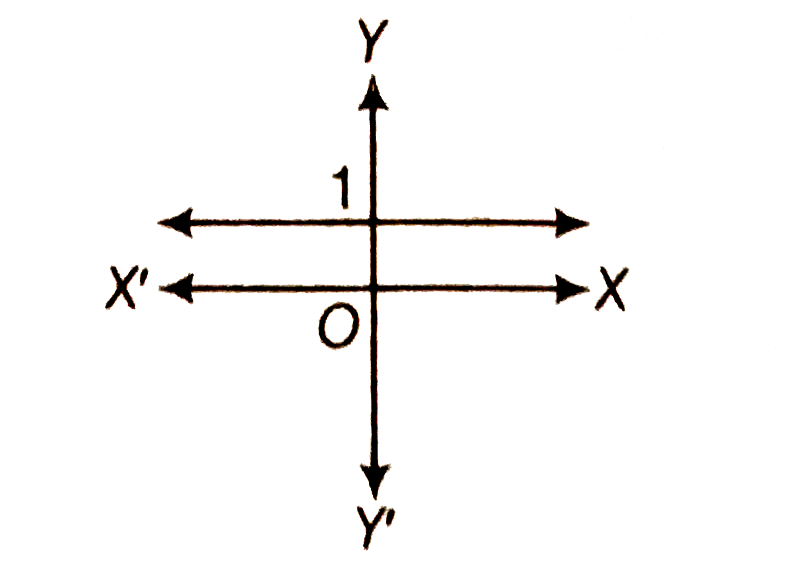
(xii) Graph of $y \leq 0$ is

(xiii) Solution set of $x \leq 0 and y \leq 0$ is

(xiv) Solution set of $x \geq 0 and y \leq 1$ is

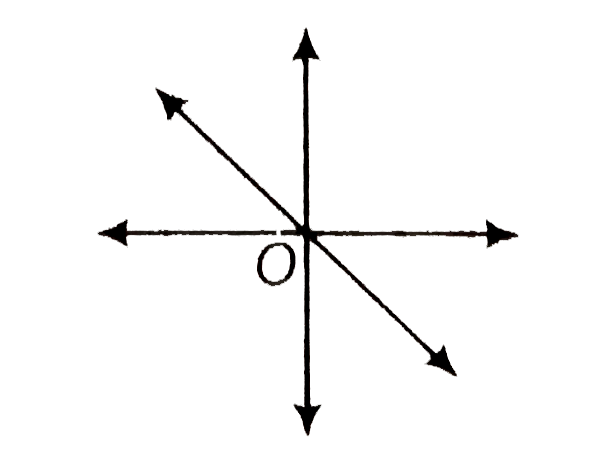
(xv) Solution set of $x + y \geq 0$ is

Text Solution

Verified by Experts

(i) If $x < y and b < 0$
$\Rightarrow \frac{x}{b} > \frac{y}{b}$
Hence, statement (i) is false.
(ii) If $x y > 0, then 0, y > 0 or x < 0, y < 0$ .
Hence, statement (ii) is true.
(iii) If $x y > 0, then x < 0 and y < 0$ .
Hence, statement (iii) is true.
(iv) If $x y < 0 \Rightarrow x < 0, y > 0 or x > 0, y < 0$ .
Hence, statement (iv) is false.
(v) if $x < - 5 and x < - 2$ , then
$x \in (- \infty, - 5)$
Hence, statement (v) is true.
(vi) If $x < - 5 and x > 2$ , then x have no value.
Hence, statement (vi) is false.
(vii) If $x > - 2 and x < 9, then x \in (- 2, 9)$ .
Hence, statement (vii) is true.
(viii) If $| x | > 5, then either x < - 5 or x > 5$ .
$\Rightarrow x \in (- \infty, - 5) \cup (5, \infty)$
Hence, statement (viii) is false.
(ix) If $| x | \leq 4$ , then
$- 4 \leq x \leq 4$
$\Rightarrow x \in [- 4, 4]$
Hence, statement (ix) is true.
(x) The given graph represents $x \leq 3$ .
Hence, statement (x) is false.
(xi) The given graph represents $x \geq 0$ .
Hence, statement (xi) is true.
(xii) The given graph represent $y \geq 0$ .
Hence, statement (xii) is false.
(xiii) Solution set of $x \geq 0 and y \leq 0$ is

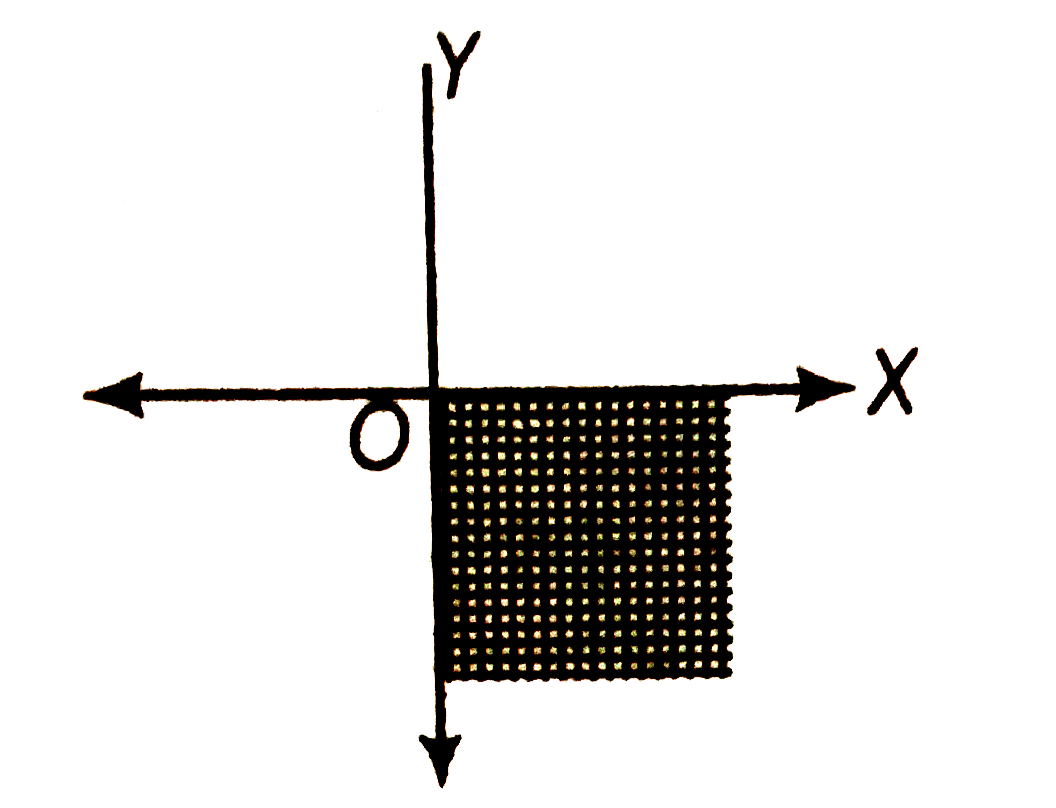
Hence, statement (xiii) is false.
(xiv) Solution set of $x \geq 0 and y \leq 1$ is

Hence, statement (xiv) is false.
(xv) The given graph represents $x + y \geq 0$ .
Hence, statement (xv) is correct.

Updated on:21/07/2023

If $x y < 0$ , which of the following must be true?
I. $x + y = 0$
II. $2 x - 2 y < 0$
III. $x^{2} + y^{2} > 0$
AI only
BIII only
CI and III
DII and III
If $0 \leq x \leq 360^{\circ}, tan x < 0 and cos x tan x > 0$ , then which of the following is a possible value for x?
A $30^{\circ}$
B $150^{\circ}$
C $210^{\circ}$
D $330^{\circ}$
If $(sec x) (tan x) < 0$ , which of the following must be true?
I. tan $x < 0$
II. Csc x cot $x < 0$
III. X is in the third or fourth quadrant
AI only
BII only
CIII only
DII and III