Statement I perimeter of a regular pentagon inscribed in a circle with centre O and radius a cm equals 10asin36∘ cm.
Statement II Perimeter of a regular polygon inscribed in a circle with centre O and radius a cm equals (3n−5)sin(360∘2n)cm, then it is n sided, where n≥3. Solution in Punjabi
(a)Both Statement I and Statement II are correct and Statement II is the correct explanation of Statement I
(b)Both Statement I and Statement II are correct and Statement II is not the correct explanation of Statement I
(c)Statement I is correct but Statement II is incorrect
(d)Statement I is correct but Statement I is incorrect
The correct Answer is:C
Step by step video & image solution for Statement I perimeter of a regular pentagon inscribed in a circle with centre O and radius a cm equals 10a sin 36^(@) cm. Statement II Perimeter of a regular polygon inscribed in a circle with centre O and radius a cm equals (3n-5)sin ((360^(@))/(2n))cm, then it is n sided, where n ge3. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Passage Based Questions)
25 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 5: MATCHING TYPE QUESTIONS
4 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (More Than One Correct Option Type Questions)
24 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Find dydx,ify=500e7x+600e−7x
View SolutionMatch the statement of Colume I with values of Column II.
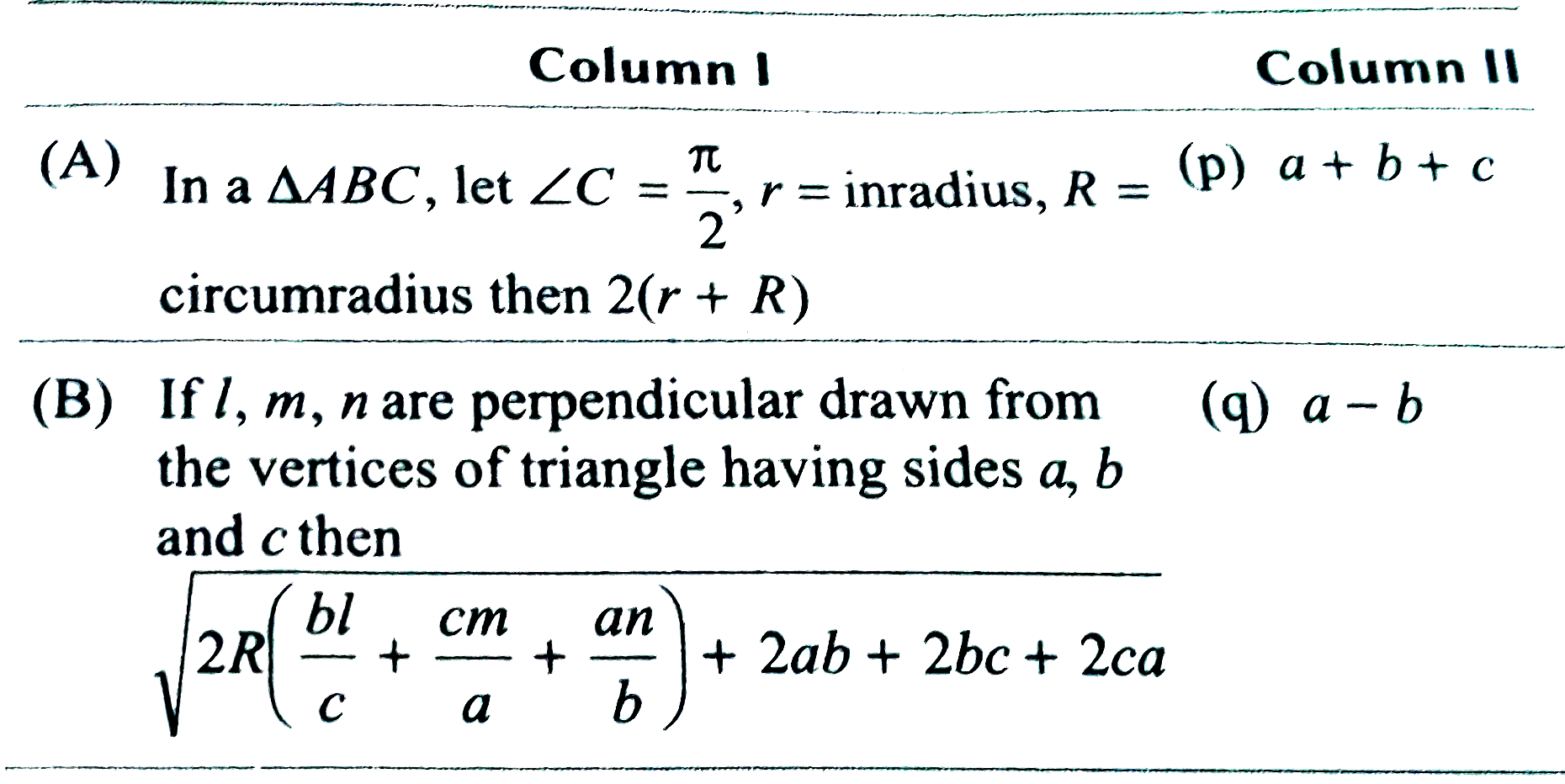
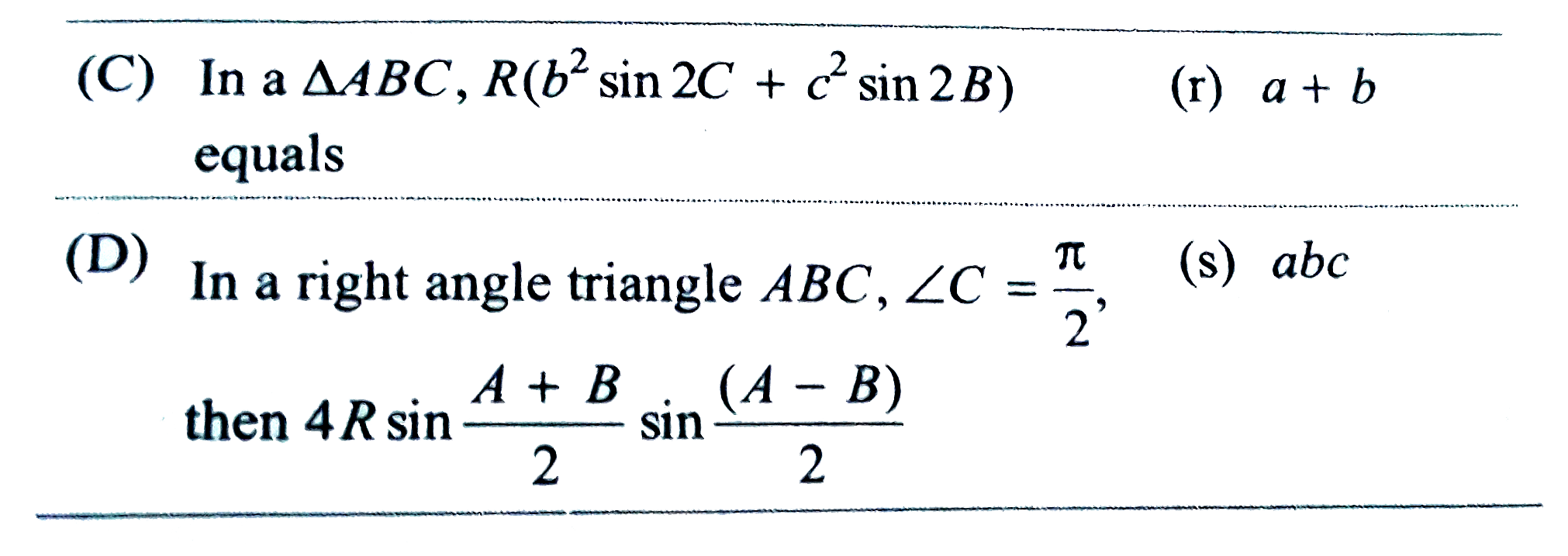
View SolutionIf area of ΔABC(Δ) and angle C are given and if c opposite to given angle is minimum, then
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionIn the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
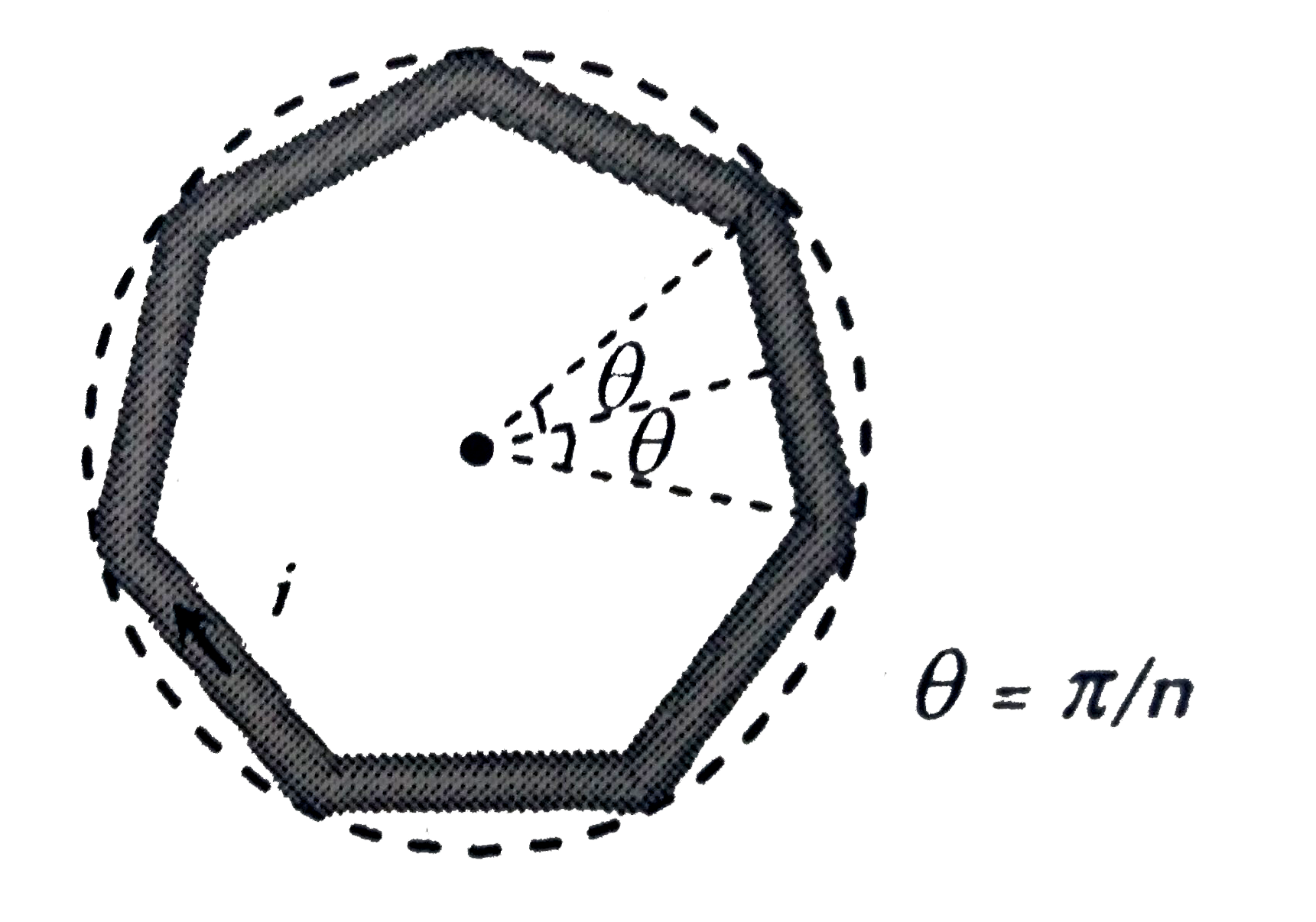
View SolutionIf r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
View SolutionFind the perimeter of
(i) a regular pentagon of side 8 cm.
(ii) a regular octagon of side 4.5 cm.
(iii) a regular decagon of side 3.6 cm.
View SolutionWhat is the perimeter of regular pentagon if side is 4 cm
View SolutionFind the perimeter of a regular octagon in inscribed in a circle of radius 100 cm:
View SolutionA ABC is inscribed in a circle with centre o and radius 5 cm and AC is a diameter of the circle. If AB = 8 cm, then BC = ......... cm.
View SolutionA ABC is inscribed in a circle with centre o and radius 5 cm and AC is a diameter of the circle. If AB = 8 cm, then BC = ......... cm.
View Solutionकथन-।: वृत्त जिसका केन्द्र 0 तथा त्रिज्या r सेमी है, के अन्तर्गत समपंचभुज का परिमाप 10asin36∘ सेमी होगा। क्योंकि कथन-II: वृत्त जिसका केन्द्र तथा त्रिज्या a सेमी है, के अन्तर्गत समबहुभुज का परिमाप (3a -5) sin 360∘2n सेमी होगा, तब यह n भुजाओं वाला होगा, जहाँ n≥3 है।
View SolutionIn the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a . Net magnetic field at centre will be
View SolutionA regular dodecagon is inscribed in a circle of radius 1 cm. find the area of the dodecagon.
View SolutionThe area of the circle and the area of a regular polygon inscribed the circle of n sides and of perimeter equal to that of the circle are in the ratio of
View Solution
