Statement I In any triangle ABC, the square of the length of the bisector AD is bc(1−a2(b+c)2).
Statement II In any triangle ABC length of bisector AD is 2bc(b+c)cos(A2). Solution in Punjabi
(a)Both Statement I and Statement II are correct and Statement II is the correct explanation of Statement I
(b)Both Statement I and Statement II are correct and Statement II is not the correct explanation of Statement I
(c)Statement I is correct but Statement II is incorrect
(d)Statement I is correct but Statement I is incorrect
The correct Answer is:A
Step by step video & image solution for Statement I In any triangle ABC, the square of the length of the bisector AD is bc(1-(a^(2))/((b+c)^(2))). Statement II In any triangle ABC length of bisector AD is (2bc)/((b+c))cos ((A)/(2)). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Passage Based Questions)
25 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 5: MATCHING TYPE QUESTIONS
4 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (More Than One Correct Option Type Questions)
24 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Find dydx,ify=500e7x+600e−7x
View SolutionMatch the statement of Colume I with values of Column II.
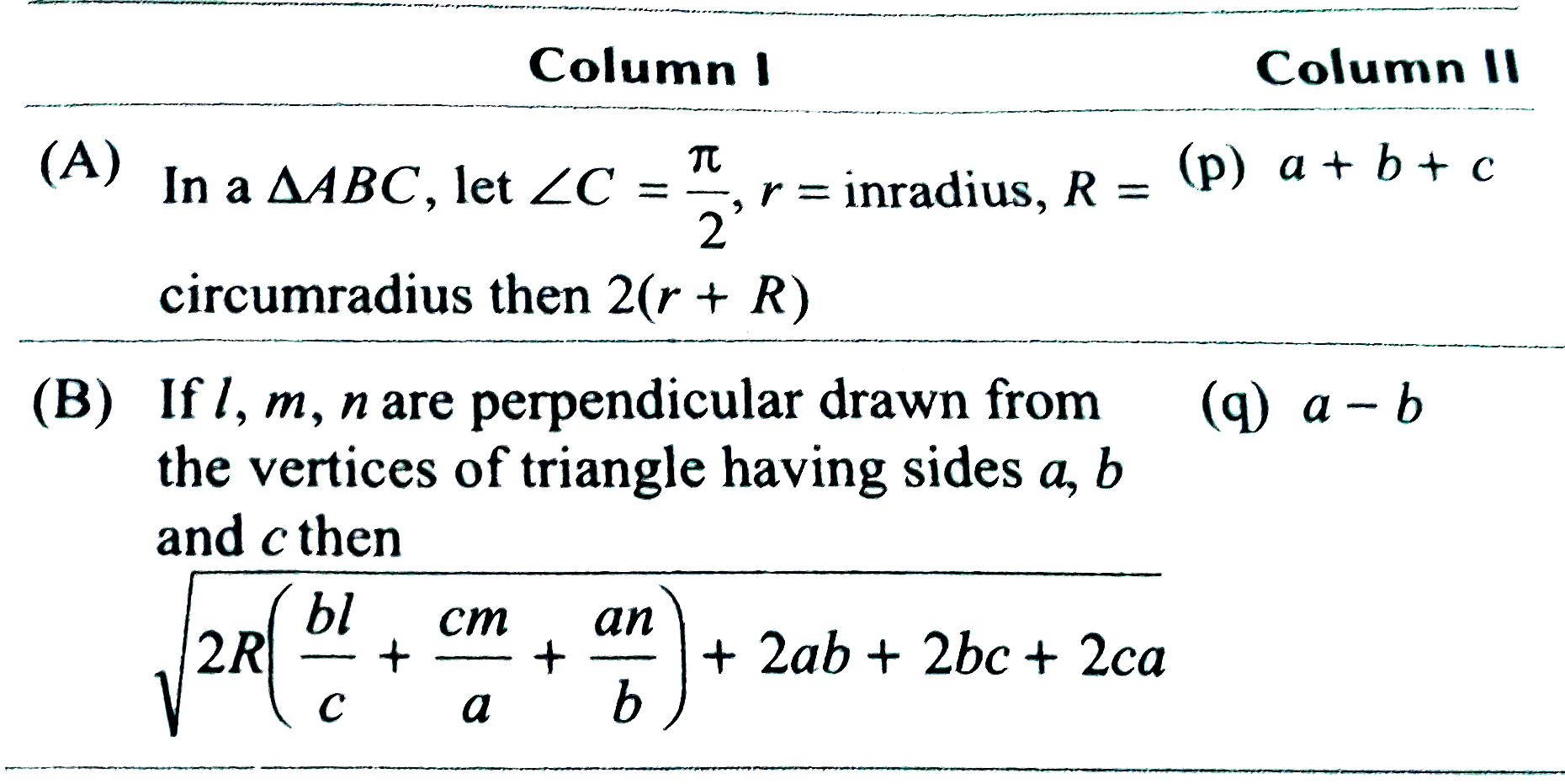
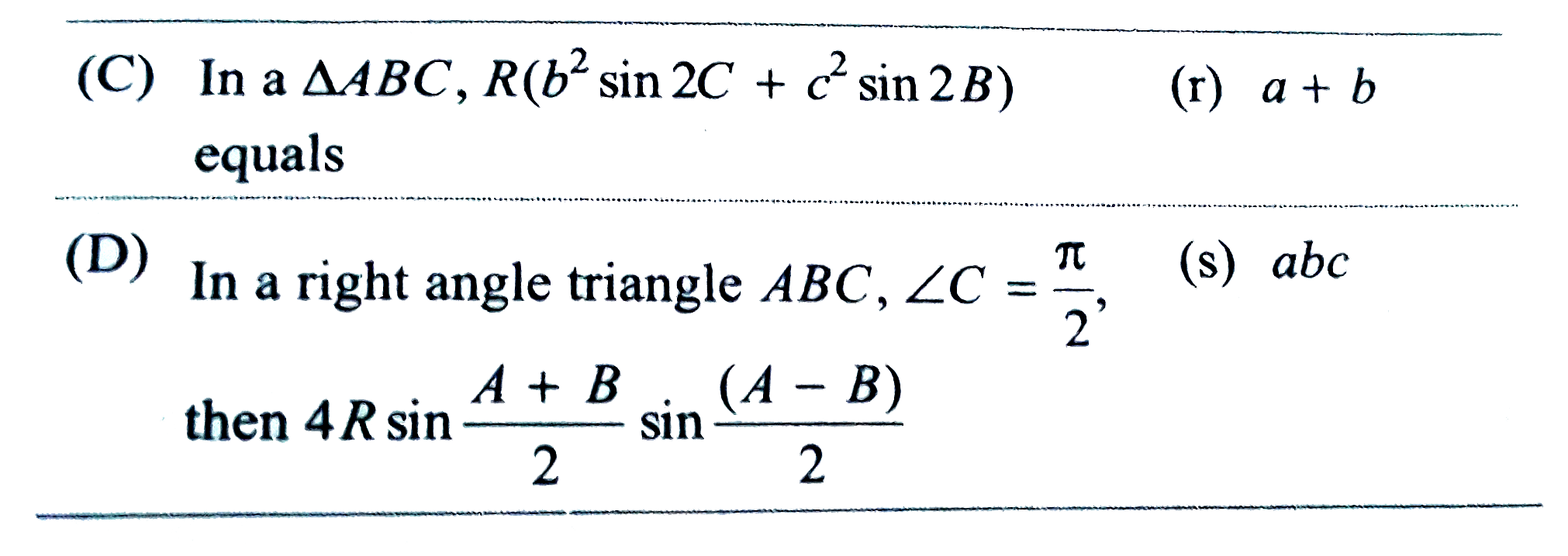
View SolutionIf area of ΔABC(Δ) and angle C are given and if c opposite to given angle is minimum, then
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
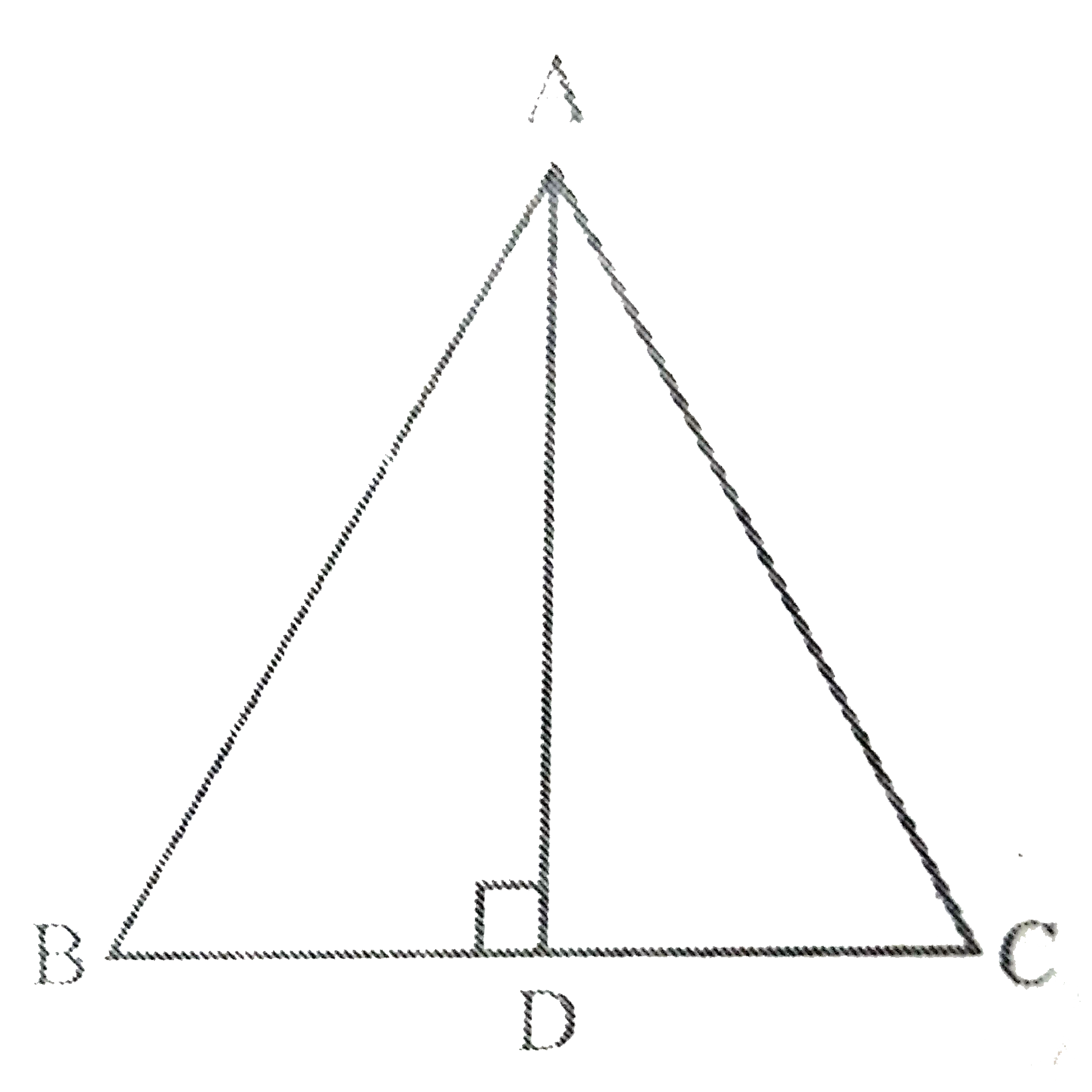
View SolutionIn ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
View SolutionIf the bisector of the angle A of triangle ABC meets BC in D, prove that a=(b+c)[1-([AD]^(2))/(bc)]^((1)/(2))
View SolutionIf AD,BE,CF are internal bisectors of the angles of ΔABC then cos(A2)AD+cos(B2)BE+cos(C2)CF=
View SolutionIf in a triangle ABC,bc2cosA=b2+c2−2bccosA then prove that the triangle must be isosceless
View SolutionIf the lengths of the sides BC, CA and AB of ΔABC are a,b, and c repspectively and AD is the bisector of ∠A then find the length of BD and DC.
View SolutionStatement I In any triangle ABC
acosA+bcosB+ccosC≤s.
Statement II In any triangle ABC
sin(A2)sin(B2)sin(C2)≤18
View Solutionत्रिभुज ABC में ∠A कि अर्द्धक रेखा BC से बिंदु D पर मिलती है । सिद्ध कीजिए कि -
AD=2bcb+ccos.A2
View SolutionIn a triangle ABC the length of the bisector of angle A is :
(i) 2bcb+csin.A2
(ii) 2bcb+ccos.A2
(iii) abc2R(b+c)cosec.A2
(iv) 4Ab+ccosec.A2
View Solutionযে কোনো ত্রিভুজের ABC -তে ভেক্টর পদ্ধতির প্রয়োগে প্রমান করো যে, a2=b2+c2−2bccosA, যেখানে ABC ত্রিভুজের A,B,C কোণের বিপরীত বাহুর দৈর্ঘ্য যথাক্রমে a,b,c ।
View SolutionIn ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.

View SolutionIf in a triangle ABC,bc2cosA=b2+c2−2bccosA then prove that the triangle must be isosceles.
View Solution
