The along side figure shows a parallelogram ABCD in which AE = EF = FC.
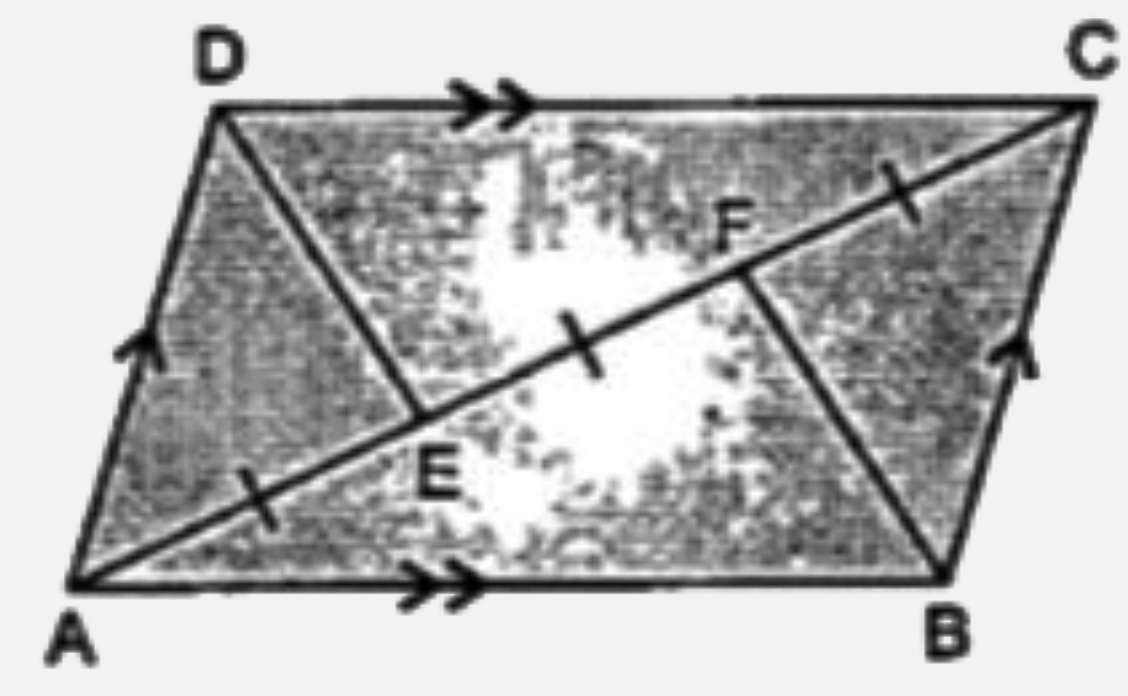
Prove that :
(i) DE is parallel to FB
(ii) DE = FB
(iii) DEBF is a parallelogram
Step by step video & image solution for The along side figure shows a parallelogram ABCD in which AE = EF = FC. Prove that : (i) DE is parallel to FB (ii) DE = FB (iii) DEBF is a parallelogram by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - QUADRILATERALS AND ITS PROPERTIES - 3 MARKS QUESTIONS
8 Videos
- RATIONAL AND IRRATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (D)
21 Videos
- SIMULTANEOUS EQUATIONSBOOK - ICSECHAPTER - SIMULTANEOUS EQUATIONSEXERCISE - EXERCISE 6 (G)
13 Videos
Similar Questions
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD= BC
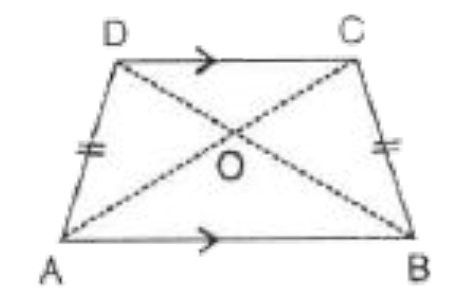
Prove that:
∠ADC=∠BCD
View SolutionThe following figure shows a trapezium ABCD in which AB is parallel to DC and AD= BC

Prove that:
∠DAB=∠CBA
View SolutionThe following figure shows a trapezium ABCD in which AB is parallel to DC and AD= BC

Prove that:
OA = OB and OC= OD
View SolutionThe adjoining figure shows a parallelogram ABCD in which P is mid-point of AB and Q is mid-point of CD. Prove that AE=EF=FC.
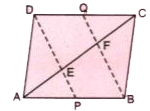
View SolutionThe given figure shows a rectangle ABDC and a parallelogram ABEF, drawn on opposite sides of AB. Prove that :
(i) quadrilateral CDEF is a parallelogram, (ii) Area of quad. CDEF
= Area of rec. ABDC
+Area of//gm.ABEF.
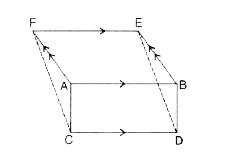
View SolutionThe following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC.
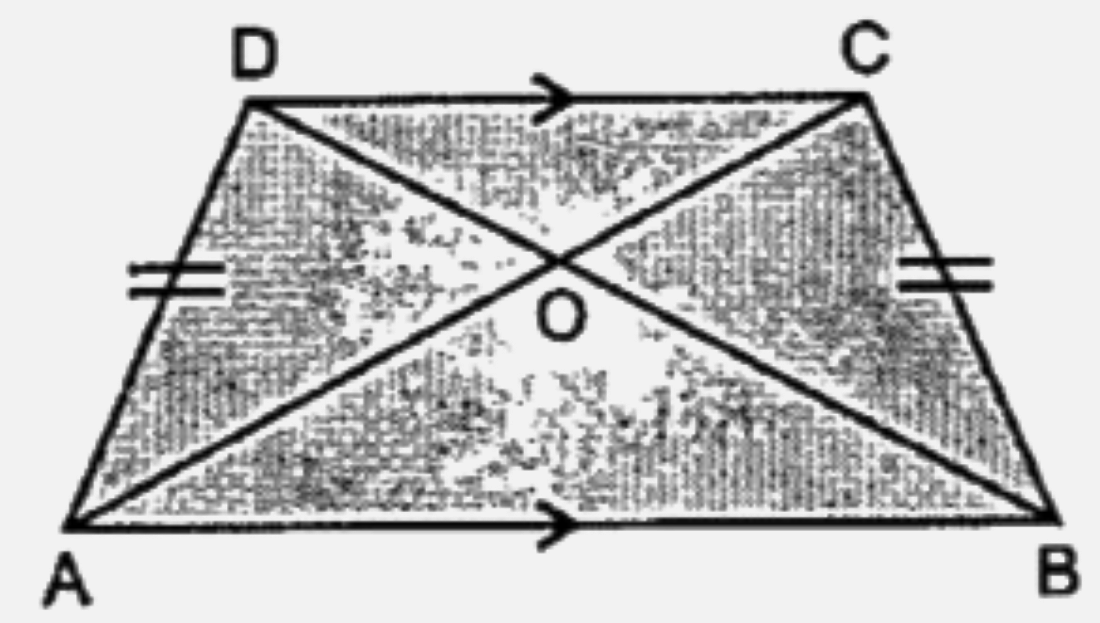
Prove that :
(i) ∠DAB=∠CBA
(ii) ∠ADC=∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD
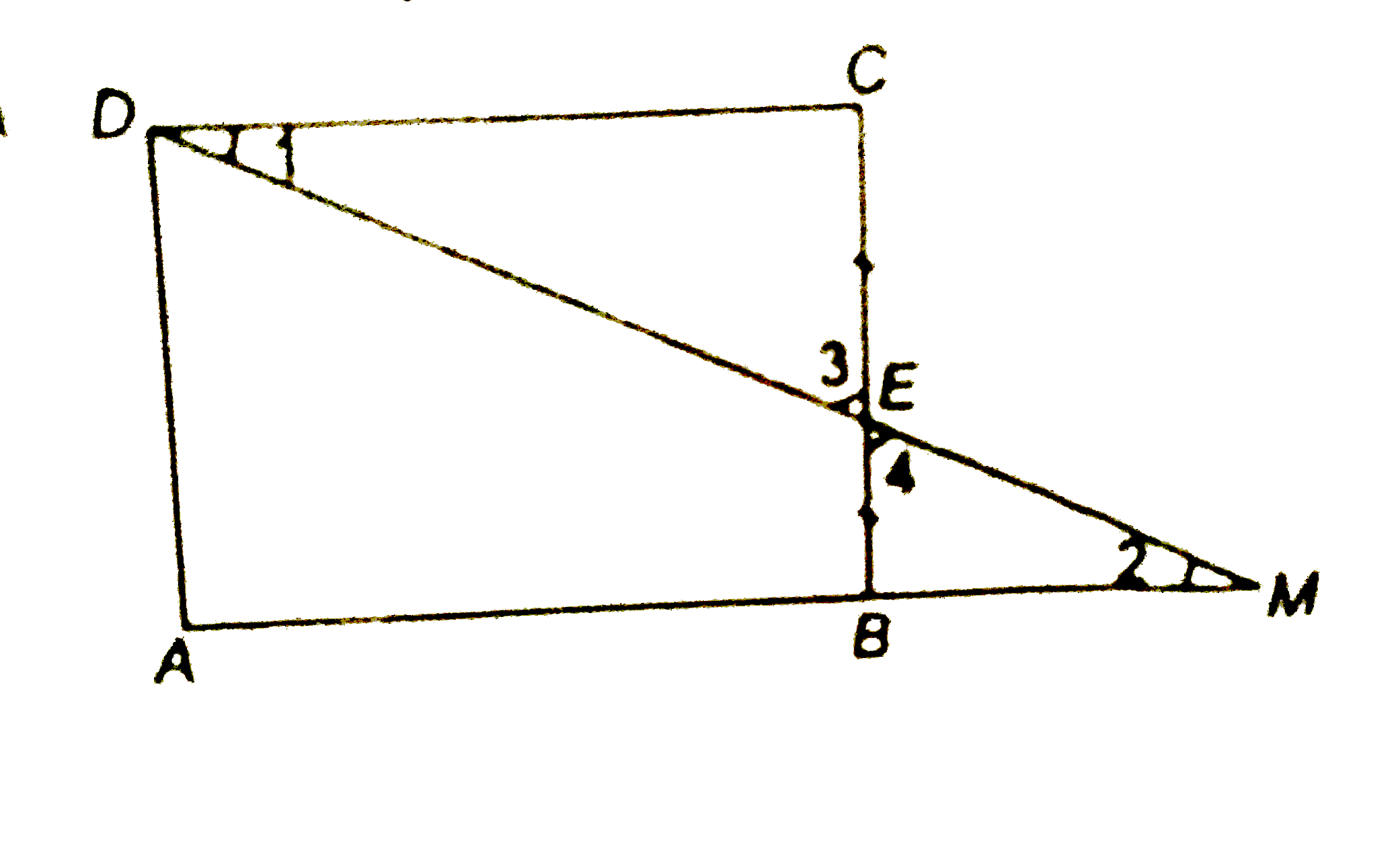
View SolutionIn the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
View SolutionThe given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM=BN
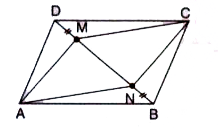 .
.
Prove that:
(i) ΔDMC≅ΔBNA and so CM=AN.
(ii) ΔAMD≅ΔCNB and so AM=CN.
(iii) ANCM is a parallelogram.
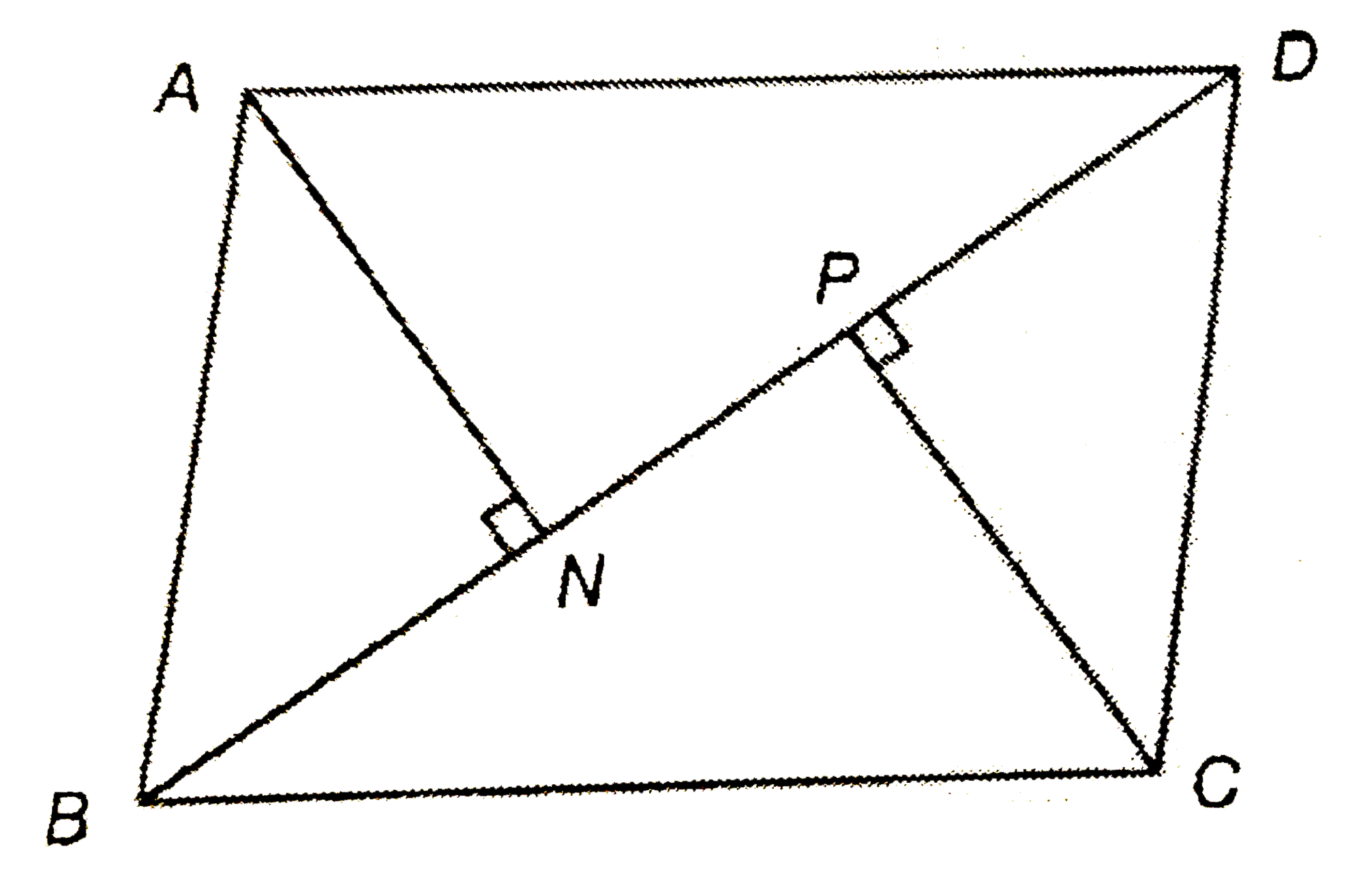
View SolutionIn the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
View SolutionIn parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that:
(i) AX=YC.
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
View Solution
