The angle between the pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α . then the equation of the locus of the point P is Solution in Tamil
x2+y2+4x−6y+4=0
x2+y2+4x−6y−9=0
x2+y2+4x−6y−4=0
x2+y2+4x−6y+9=0
The correct Answer is:4
The center of the circle
x2+y2+4x−6y+9sin2α+13cos2α=0
is C(−2,3) and its radius is
√4+9−9sin2α−13cos2α=|2sinα|
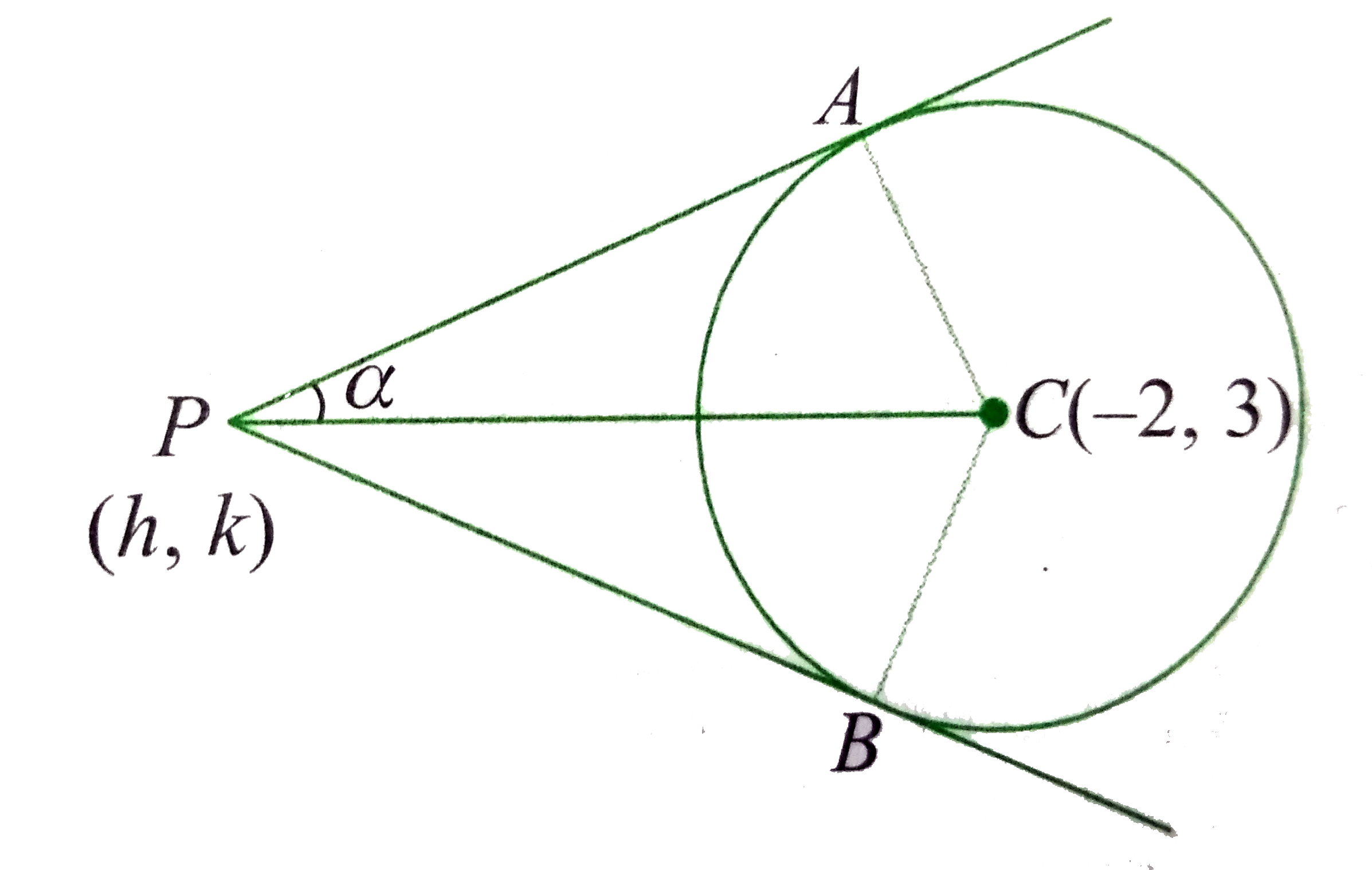
Let P(h,k) be any point on the locus . Then ∠APC=α
From the diagram,
sinα=ACPC=2sinα√(h+2)2+(k−3)2
or (h+2)2+(k−3)2=4
or h2+k2+4h−6k+9=0
Thus, the required equation of the locus is
x2+y2+4x−6y+9=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionThe angle between the pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α . then the equation of the locus of the point P is x2+y2+4x−6y+4=0 x2+y2+4x−6y−9=0 x2+y2+4x−6y−4=0 x2+y2+4x−6y+9=0
View SolutionThe angle between a pair of tangents from a point P to the circe x^(2)+y^(2)+4x-6y+9sin2 alpha+13cos^(2)alpha=0 is 2 alpha. Find the equation of the locus of the point P.
View SolutionThe locus of a moving point so that tangents from it to circle x2+y2+4x−6y+9sin2α+13cos2α=0 are inclined at an angle '2α'Find the equation of the locus of the point . :
View SolutionThe angle between a pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α. The equation of the locus of the point P is
View SolutionThe angle between a pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α. The equation of the locus of the point P is
View Solutionबिन्दु P से वृत्त x2+y2+4x−6y+9sin2α+13cos2α=0 पर खींची गई स्पर्शी युग्म की स्पार्शियों के मध्य 2α कोण बनाता है , तो बिन्दु P का बिन्दुपथ है
View SolutionThe angle between a pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α. The equation of the locus of the point P is
View SolutionAngle between a pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2θ+13cos2θ=0 is 2θ . Then the locus of P is:
View SolutionThe angle between a pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α. The equation of the locus of the point P is
View SolutionIf from any point P on the circle x2+y2+2gx+2fy+c=0, tangents are drawn to the circle x2+y2+2gx+2fy+csin2α+(g2+f2)cos2α=0 , then find the angle between the tangents.
View SolutionThe angle between the pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α . then the equation of the locus of the point P is a. x2+y2+4x−6y+4=0 b. x2+y2+4x−6y−9=0 c. x2+y2+4x−6y−4=0 d, x2+y2+4x−6y+9=0
View Solution
