The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60∘. Find the angles of the parallelogram.
Let the parallelogram be ABCD, in which ∠ADCand∠ABC are obture angles. Now, DE and DF are two altitudes of parallelogram and angles between them is 60∘.
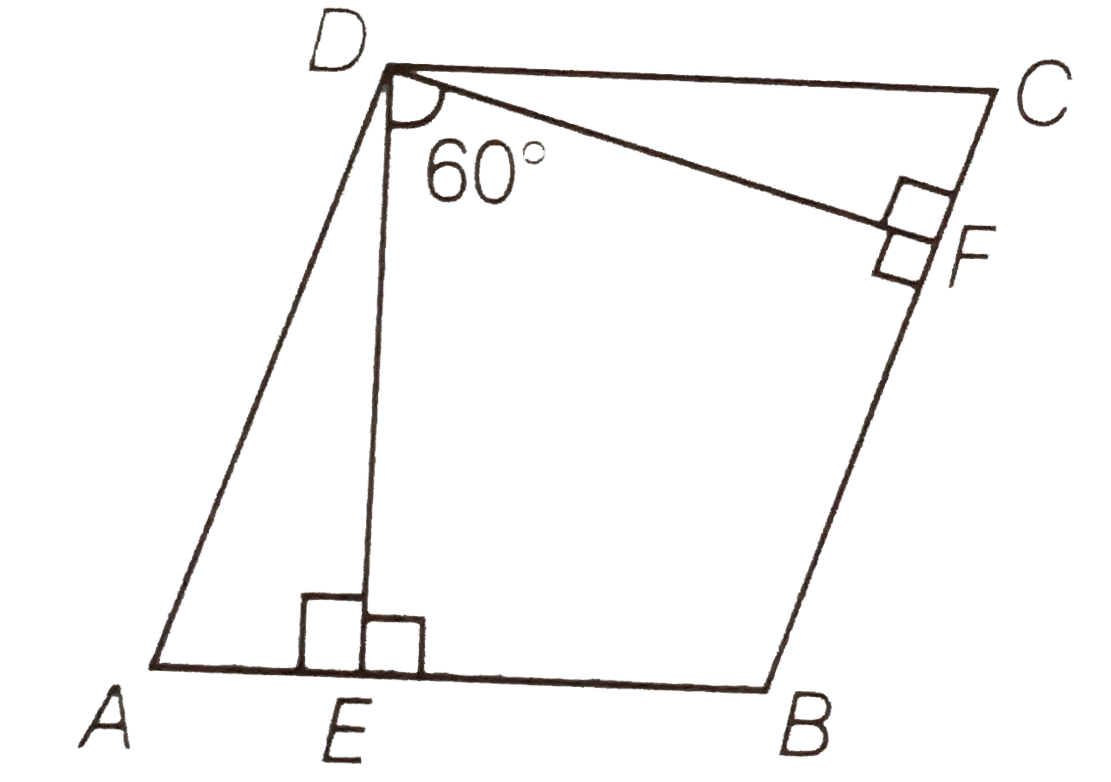
Now, BEDF is a quadrilateral, in which ∠BED=∠BFD=90∘
∴ ∠FBE=360∘−(∠FDE+∠BED+∠BFD)
∴ ∠FBE=360∘−(∠FDE+∠BED+∠BFD)
=360∘−240∘=120∘
Since, ABCD is parallelogram. ltBrgt ∴ ∠ADC=120∘
Now, ∠A+∠B=180∘ [sum of two cointerior angles is 180∘] ltBrgt ∴ ∠A=180∘−∠B
5=180∘−120∘ [∵∠FBE=∠B] ltBrgt ⇒ ∠A=60∘
Also, ∠C=∠A=60∘
Hence, angles of the parallelogram are 60∘,120∘,60∘and120∘, respectively.
Topper's Solved these Questions
Similar Questions
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
View SolutionThe angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 600. Find the angles of parallelogram.
View Solution
Knowledge Check
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle is 50∘ . The two adjacent angles of parallelogram are
A50∘,130∘B60∘,120∘C55∘,125∘D70∘,110∘Consecutive angles of parallelogram are
AEqualBComplimentaryCSupplementaryDNone of these
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is
View SolutionThe sum of two opposite angles of a parallelogram is 130∘. Find all the angles of the parallelogram.
View SolutionOne angle of a parallelogram is 60∘. Find its remaining angles.
View SolutionABCD is a parallelogram, where, One of the angles of the parallelogram is 60∘ .Find all other angles.
View SolutionThe sum of adjacent angles of a parallelogram is
View SolutionThe ratio of measure of two adjacent angle of parallelogram is 1:2. Find the measure of all angles of the parallelogram.
View Solution
