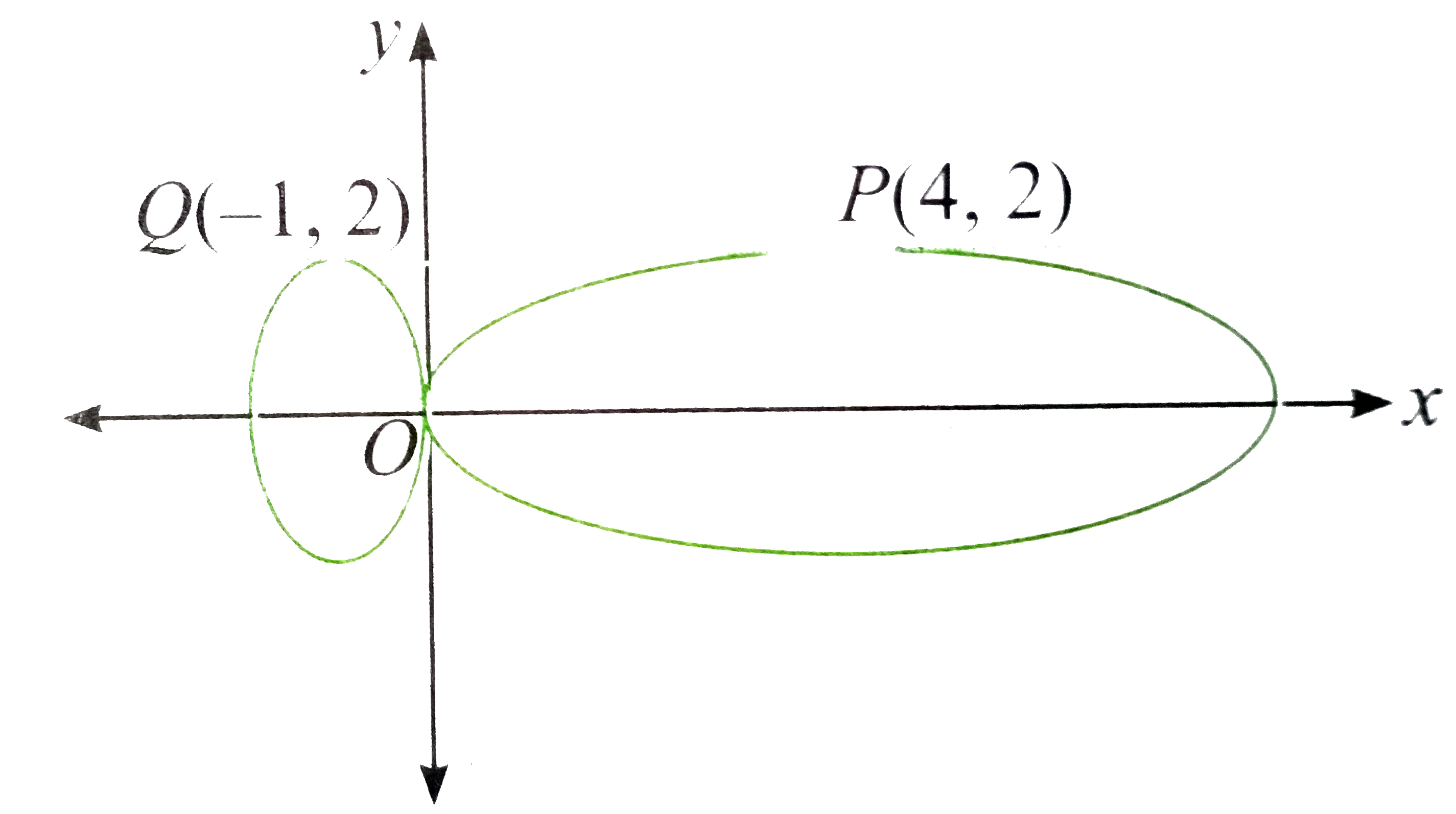
The angle subtended by common tangents of two ellipses 4(x-4)^2+25 y^2

The number of common tangents to the ellipse $\frac{x^{2}}{16} + \frac{y^{2}}{9} = 1$ and the circle $x^{2} + y^{2} = 4$ is
A2
B1
C0
D4
The length of the common tangent to the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{4}$ = 1 and the circle $x^{2} + y^{2} = 16$ intercepted by
A5
B $2 \sqrt{7}$
C $\frac{7}{\sqrt{3}}$
D $\frac{14}{\sqrt{3}}$
The equation of common tangent of the curve $x^{2} + 4 y^{2} = 8$ and $y^{2} = 4 x$ are
A $x - 2 y + 4 = 0$
B $x + 2 y + 4 = 0$
C $2 x - y + 4 = 0$
D $2 x + y + 4 = 0$

The angle subtended by common tangents of two ellipses $4 {(x - 4)}^{2} + 25 y^{2} = 100$ and $4 {(x + 1)}^{2} + y^{2} = 4$ at the origin is