The number of common tangents to the ellipse x216+y29=1 and the circle x2+y2=4 is
2
1
0
4
The correct Answer is:C
To find the number of common tangents to the ellipse x216+y29=1 and the circle x2+y2=4, we can follow these steps:
Step 1: Identify the equations of the ellipse and the circle
The given ellipse is:
x216+y29=1
This can be rewritten in standard form where a2=16 and b2=9.
The given circle is:
x2+y2=4
This can be rewritten as x2+y2=r2 where r2=4 implies r=2.
Step 2: Write the equation of the tangent to the circle
The equation of the tangent to the circle at a slope m is given by:
y=mx±√r2(1+m2)
Substituting r2=4:
y=mx±√4(1+m2)=mx±2√1+m2
Step 3: Write the equation of the tangent to the ellipse
The equation of the tangent to the ellipse at a slope m is given by:
y=mx±√a2m2+b2
Substituting a2=16 and b2=9:
y=mx±√16m2+9
Step 4: Set the two tangent equations equal to each other
For the tangents to be common, we set the two equations equal:
mx±2√1+m2=mx±√16m2+9
We can ignore mx since it is common on both sides. This leads to two cases:
1. 2√1+m2=√16m2+9
2. −2√1+m2=√16m2+9 (This case will not yield valid solutions since the left side is negative.)
Step 5: Solve the equation
From the first case:
2√1+m2=√16m2+9
Squaring both sides:
4(1+m2)=16m2+9
Expanding and rearranging:
4+4m2=16m2+9
4−9=16m2−4m2
−5=12m2
m2=−512
Step 6: Analyze the result
Since m2 cannot be negative, this indicates that there are no real values for m. Therefore, there are no common tangents to the ellipse and the circle.
Conclusion
The number of common tangents to the ellipse and the circle is 0.
---
The given ellipse is:
x216+y29=1
This can be rewritten in standard form where a2=16 and b2=9.
x2+y2=4
This can be rewritten as x2+y2=r2 where r2=4 implies r=2.
The equation of the tangent to the circle at a slope m is given by:
y=mx±√r2(1+m2)
Substituting r2=4:
y=mx±√4(1+m2)=mx±2√1+m2
The equation of the tangent to the ellipse at a slope m is given by:
y=mx±√a2m2+b2
Substituting a2=16 and b2=9:
y=mx±√16m2+9
For the tangents to be common, we set the two equations equal:
mx±2√1+m2=mx±√16m2+9
We can ignore mx since it is common on both sides. This leads to two cases:
1. 2√1+m2=√16m2+9
2. −2√1+m2=√16m2+9 (This case will not yield valid solutions since the left side is negative.)
From the first case:
2√1+m2=√16m2+9
Squaring both sides:
4(1+m2)=16m2+9
Expanding and rearranging:
4+4m2=16m2+9
4−9=16m2−4m2
−5=12m2
m2=−512
Since m2 cannot be negative, this indicates that there are no real values for m. Therefore, there are no common tangents to the ellipse and the circle.
The number of common tangents to the ellipse and the circle is 0.
Topper's Solved these Questions
- CONIC SECTIONSBook:AAKASH INSTITUTE ENGLISHChapter:CONIC SECTIONSExercise:SECTION-C ( Objective Type Questions ( More than one answer))
Explore 1 Video
- CONIC SECTIONSBook:AAKASH INSTITUTE ENGLISHChapter:CONIC SECTIONSExercise:SECTION-C
Explore 44 Videos
- CONIC SECTIONSBook:AAKASH INSTITUTE ENGLISHChapter:CONIC SECTIONSExercise:Assignment (SECTION - A)
Explore 55 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:AAKASH INSTITUTE ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:section-J (Aakash Challengers Qestions)
Explore 13 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:AAKASH INSTITUTE ENGLISHChapter:CONTINUITY AND DIFFERENTIABILITYExercise:section - J
Explore 6 Videos
Similar Questions
If L be the length of common tangent to the ellipse x225+y24=1 and the circle x2+y2=16 intercepted by the coordinates axis then √3L2 is _____
View SolutionThe minimum length of intercept on any tangent to the ellipse x24+y29=1 cut by the circle x2+y2=25 is :
View SolutionThe equation of common tangents to the ellipse x2+2y2=1 and the circle x2+y2=23 is
View SolutionThe minimum area of the triangle formed by the tangent to the ellipse x216+y29=1 and the co-ordinate axes is
View SolutionTwo common tangents to the circle x2+y2=a22 and the parabola y2=4ax are
View SolutionThe locus of the poles of the tangents to the ellipse x2a2+y2b2=1 w.r.t. the circle x2+y2=a2 is: (a) parabola (b) ellipse (c) hyperbola (d) circle
View SolutionThe number of common tangents to x2+y2=4,(x−3)2+(y−4)2=9 is
View SolutionStatement 1: The number of common tangents to the circles x2+y2=4 and x2+y2−6x−6y=24 is 3.
Statement 2 : If two circles touch each other externally thenit has two direct common tangents and one indirect common tangent.
View SolutionThe slopes of the common tangents of the ellipse x24+y21=1 and the circle x2+y2=3 are ±1 (b) ±√2 (c) ±√3 (d) none of these
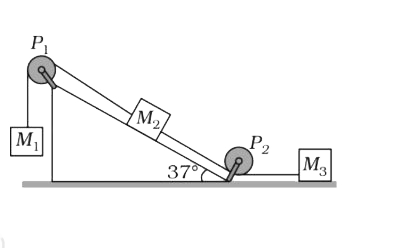
View SolutionMasses M1,M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the figure. The masses move such that the portion of the string betweenP1 and P2 is parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1 in kg
(ii) the tension in the horizontal portion of the string in Newton
View Solution
