The angles of depression of two points from the top of the tower are $30^{\circ} and 60^{\circ}$ . IF the height of the tower is 30 m, then find the maximum possible distance between the two points.

A

$40 \sqrt{3}$ m

B

$30 \sqrt{3}$ m

C

$20 \sqrt{3}$ m

D

$10 \sqrt{3}$ m

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

For the maximum possible distane, two points lie on either side of the tower.
Let AB be the height of the tower.
AB = 30 m (given)
Let P and Q be the given points
In $Δ A B P$ ,

${\tan 30}^{\circ} = \frac{A B}{P B} \Rightarrow \frac{1}{\sqrt{3}} = \frac{30}{P B} \Rightarrow P B = 30 \sqrt{3}$ .
$I n Δ A B Q, {\tan 60}^{\circ} = \frac{A B}{B Q}$
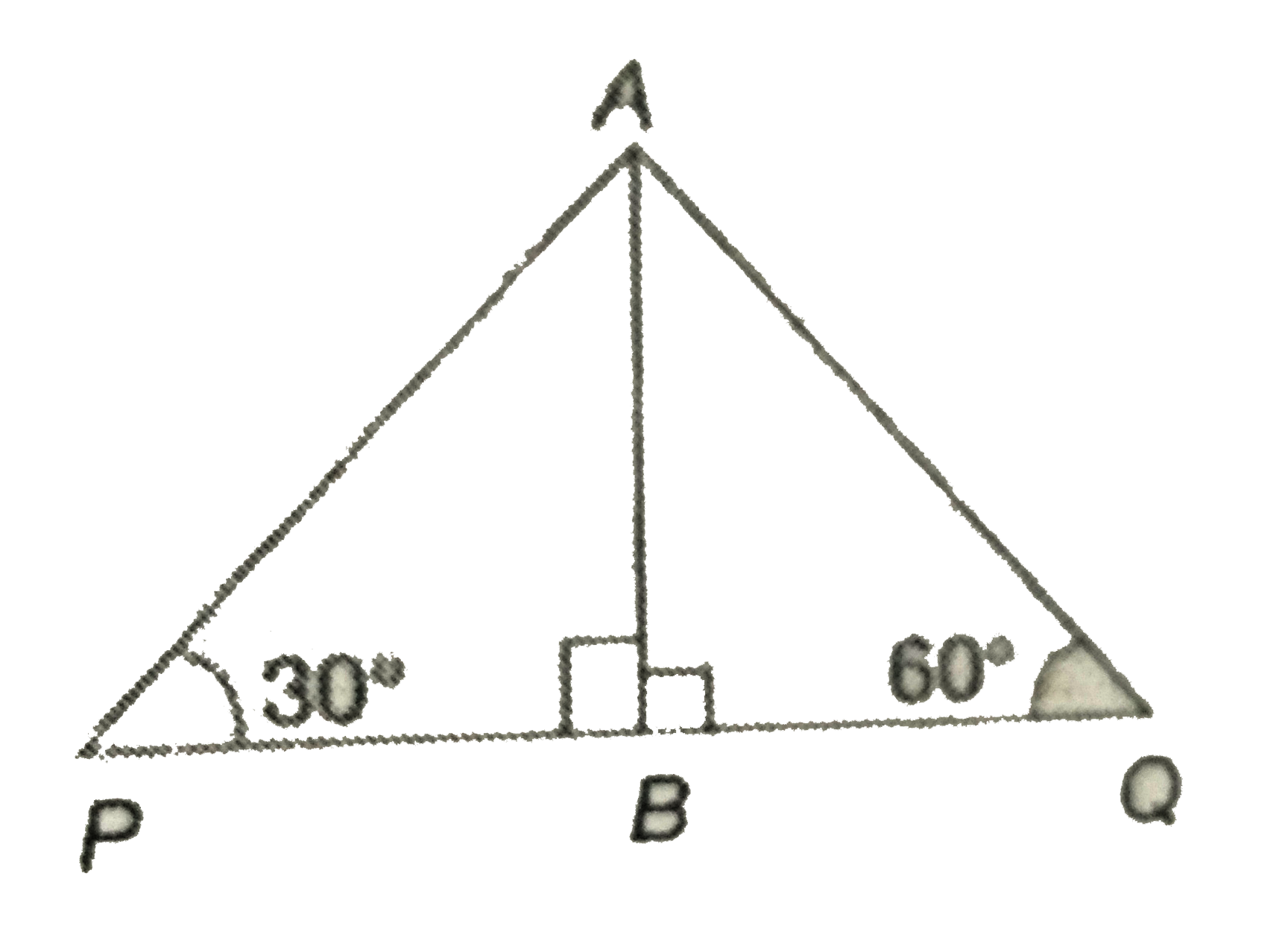
$\Rightarrow \sqrt{3} = \frac{30}{B Q} \Rightarrow B Q = \frac{30}{\sqrt{3}}$ m.
Now, PQ =PB+BQ
$= 30 \sqrt{3} + \frac{30}{\sqrt{3}} = 30 (\sqrt{3} + \frac{1}{\sqrt{3}})$
$30 (\frac{4}{\sqrt{3}}) = 40 \sqrt{3}$ m.

|

Updated on:21/07/2023

Class 10 MATHS TRIGONOMETRIC RATIOS AND IDENTITIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two men are on the opposite sides of tower. They measure the angles of elevation of the top of the tower as $45^{\circ}$ and $30^{\circ}$ . If the height of the tower is 40 m then the distance between the men is
A40m
B $40 \sqrt{3} m$
C68.280m
D109.28m
Question 2 - Select One
Two men are on the opposite sides of a tower. They measure the angles of elevation of the top of the tower as $45^{\circ}$ and $30^{\circ}$ respectively. If the height of the tower is 40 m, then the distance between the men is
A40 m
B $40 \sqrt{3} m$
C68.28 m
D109.28 m
Question 3 - Select One
The angle of depression of a point from the top of a 200 m high tower is $45^{\circ}$ . The distance of the point from the tower is
A $\frac{200}{\sqrt{3}} m$
B $200 m$
C $200 \sqrt{3}$ m
Dnone of these

PEARSON IIT JEE FOUNDATION-TRIGONOMETRY-Level 3

Home
Ask Doubt
Profile