The area bounded between the parabolas x2=y4andx2=9y and the straight line y=2 is (1) 20√2 (2) 10√23 (3) 20√23 (4) 10√2
A
20√2 sq units
B
10√23 sq units
C
20√23 sq units
D
10√2 sq units
Video Solution
Text Solution
The correct Answer is:C
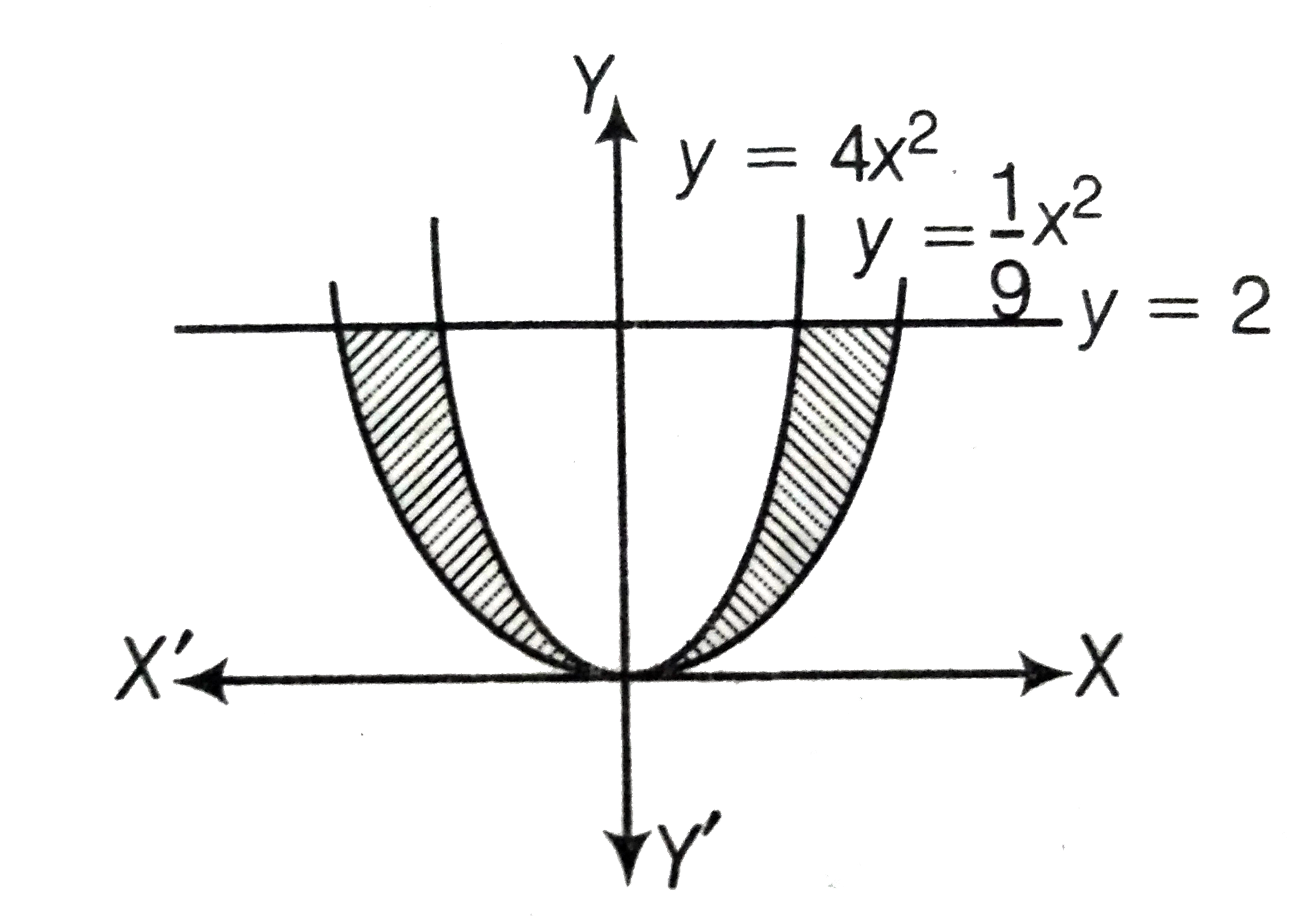
Required area
=2∫20(3√y−√y2)dy=2∫20(52√y)dy
=5⎡⎣y3/232⎤⎦y=2y=0=103(23/2−0)=20√23
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
Similar Questions
Knowledge Check
The area bounded between the parabola x2=y4 and x2=9y and the straight line y=2 is
A20√2B10√23C20√23D10√2The graph of straight line y=√3x+2√3 is :
A B
B C
C D
D
Area bounded between the curves y=√4−x2 and y2=3|x| in square units is
View SolutionThe area bounded by the curves x2+y2=4, |y|=√3x and y - axis, is
View SolutionThe area included between the parabolas y2=4ax(x+a)andy2=4b(b−x)is83√ab(a+b).True False
View Solution2√x+3√y=2 and 4√x−9√y=−1
View SolutionThe shortest distance between line y-x=1 and curve x=y2 is : (1) √34 (2) 3√28 (3) 83√2 (4) 4√3
View SolutionThe area bounded by the curve x2+y2=36and√|x|+√|y|=√6 is :
View Solution
