The area bounded by the curves y=sin−1|sinx|andy=(sin−1|sinx|)2, where 0≤x≤2π, isSolution in Tamil
13+π24 sq. units
16+π38 sq. units
2 sq. units
None of these
The correct Answer is:D
y=sin−1|sinx|=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩x,0≤x<π2π−x,π2≤x<ππ−x,π≤x<3π22π−x,3π2≤x<2π
y=(sin−1|sinx|)2=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩x2,0≤x<π2(π−x)2,π2≤x<π(x−π)2,π≤x<3π2(2π−x)2,3π2≤x<2π
The required area A is shown as shaded region in the figure.
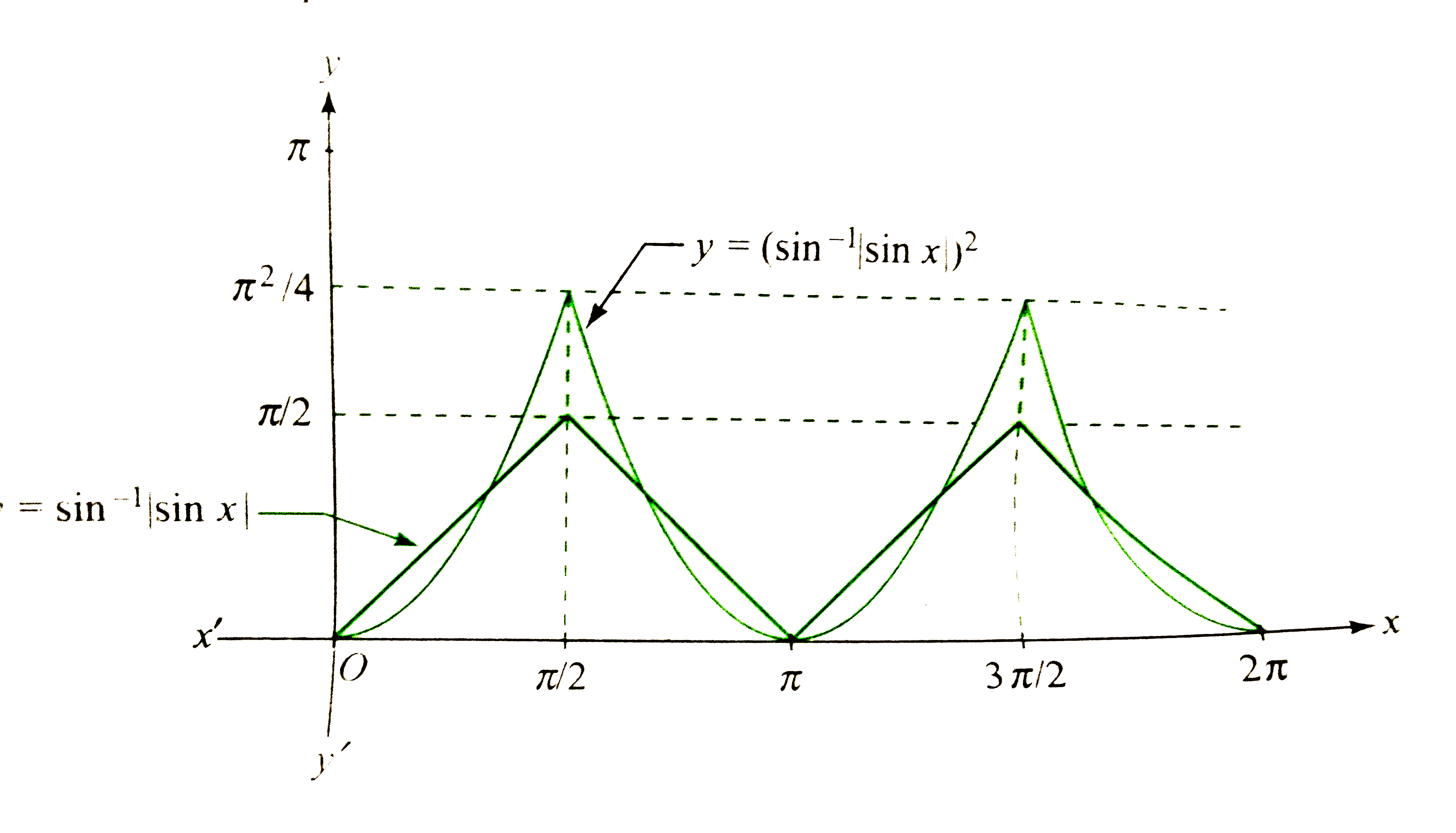
⇒ 41∫0(x−x1)dx+4π/2∫1(x2−x)dx
=43+π2[π−36] sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Let A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View SolutionLet Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratio
View SolutionFind the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y−aξs, and line x=t(where0≤t≤2).
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionThe area bounded by the curves y=sin−1|sinx|andy=(sin−1|sinx|)2, where 0≤x≤2π, is
View SolutionThe area bounded by the y-axis, y=cos x and y=sinx,0≤x≤π/4, is
View SolutionThe area bounded by the curve y=sin2x−2sinx and the x-axis, where x∈[0,2π], is
View SolutionThe equation sinx+siny+sinz=−3 for 0≤x≤2π, 0≤y≤2π,o≤z≤2π, has
View SolutionThe area bounded by the curve y=sin2x,0≤x≤π2, X axis and the line x=π2 is
View SolutionThe equation sinx+siny+sinz=−3 for 0≤x≤2π,0<y≤2π,0≤z≤2π has-
View Solutionthe equation sin x + sin y + sin z = - 3 for 0 le x le 2pi , 0 le y le 2pi , 0 le z le 2pi Of
View SolutionThe area bounded by the curves y=sin−1|sinx|andy=(sin−1|sinx|)2, where 0≤x≤2π, is
View SolutionThe area bounded by the curve y=sin2x−2sinx and the x-axis, where x∈[0,2π], is
View SolutionThe area bounded by the line y = x and y = x + sin x will be (where 0 le x le pi )
View Solution
