The area (in sq. units) of the region described by {(x,y):y2≤2x and y≥4x−1} is : (1) 732 (2) 564 (3) 1564 (4) 932Solution in Tamil
732
564
1564
932
The correct Answer is:D
y2≤2x represents the interior of parabola y2=2x (towards focus) and y≥4x−1 represents the half region of plane to the left of the line y=4x−1.
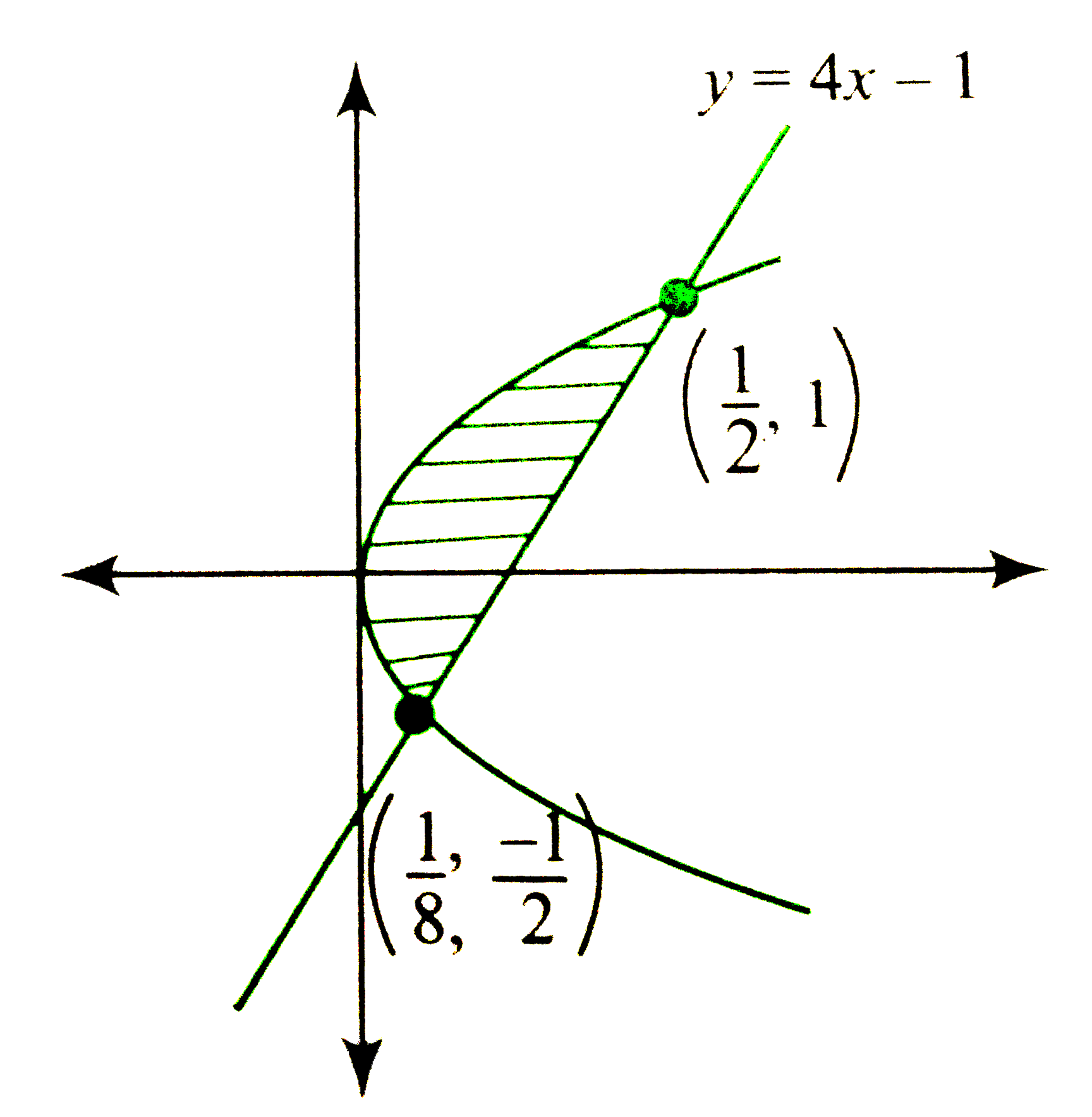
1∫−1/2(y+14−y22)dy=14{y22+y}1−1/2−16{y3}1−1/2
=14{(12+1)−(18−12)}−16{1+18}
=14{32+38}−16{98}=1532−632=932
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Single Correct Answer Type
27 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)
16 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area bounded by the curves x+2|y|=1 and x=0.
View SolutionThe area enclosed between the curve y=sin2xandy=cos2x in the interval 0≤x≤π is _____ sq. units.
View SolutionThe area enclosed by the curve C:y=x√9−x2(x≥0) and the x-axis is___.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionIf (32)x−5=(64)y+6=(256)30, then x+y=
View SolutionIf (16)2x+3=(64)x+3, then 42x−2=64(b)256(c)32(d)512
View SolutionA variable line x/a + y/b = 1 moves in such a way that the harmonic mean of a and b is 8. Then the least area of triangle made by the line with the coordinate axes is (1) 8 sq. unit (2) 16 sq. unit (3) 32 sq. unit (4) 64 sq. unit
View SolutionIf a tangent having a slope of −43 to the ellipse x218+y232=1 intersects the major and minor axes in points AandB respectively, then the area of ΔOAB is equal to (A) 12 sq. untis (B) 24 sq. units (C) 48 sq. units (D) 64 sq. units
View SolutionThe area (in sq units) of the region described by {(x,y):y2≤2xandy≥4x−1} is
View SolutionSimplify (32)1/5+(−7)0+(64)1/2
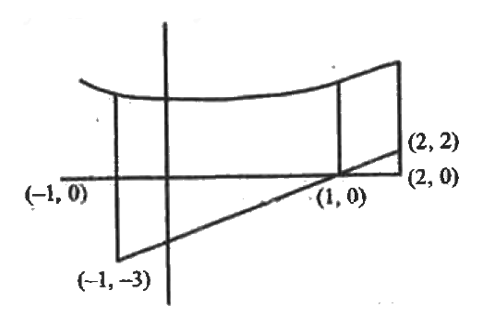
View SolutionThe area (in sq. units) of the region bounded by x=−1,x=2,y=x2+1andy=2x−2 is
View SolutionThe area (in sq. units) of the region described by : {(x,y):y2≤2x and y≥4x−1 } is :
View Solution(164)0+(64)−12+(32)45−(32)−45=?
View SolutionA variable line xa+yb=1 moves in such a way that the harmonic mean of a and b is 8. Then the least area of triangle made by the line with the coordinate axes is (1) 8 sq. unit (2) 16 sq. unit (3) 32 sq. unit (4) 64 sq. unit
View Solution
