The area (in sq units) of the region {(x,y):y2≥2xandx2+y2≤4x,x≥0,y≥0} is
π−83
π−4√23
π2−2√23
π−43
The correct Answer is:A
y2=2xandx2+y2=4x meet at O(0,0)andB(2,2){(2,−2) is not considered as x,y≥0}
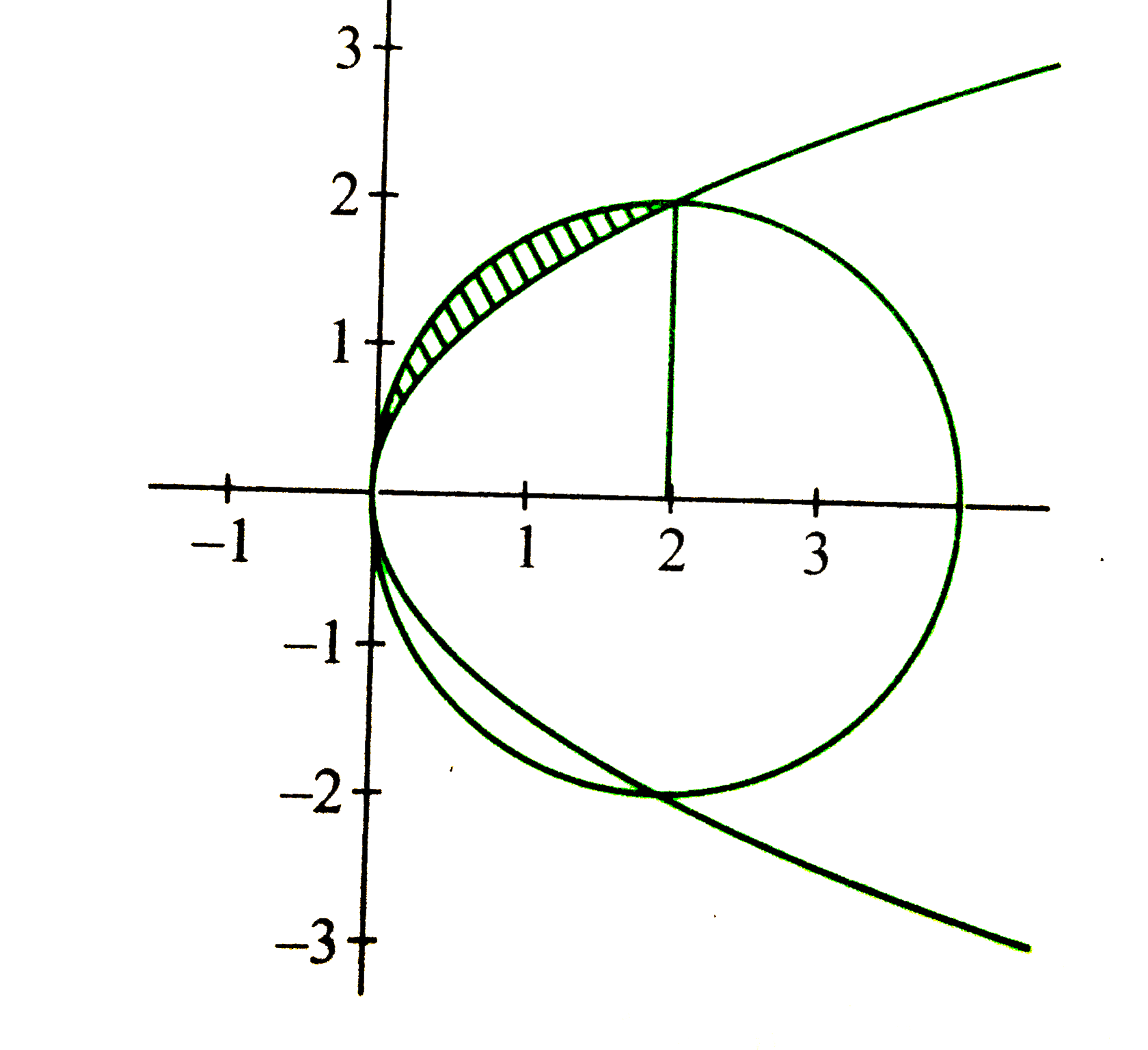
Now required area =14π×4−2∫0√2xdx
=π−√223[x3/2]20
=π−83
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type30videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answer Type3videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Numerical Value Type18videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
The area (in sq. units) of the region
{(x,y):y2≤2xandx2+y2≤4x,x≥0,y≤0},isView SolutionThe area (in sq. units) of the region
{(x,y):y2≤2xandx2+y2≤4x,x≥0,y≤0},isView SolutionThe area (in sq units) of the region A={(x,y):x2≤y≤x+2} is
View SolutionThe area (in sq units) of the region A={(x,y):x2≤y≤x+2} is
View SolutionThe area (in sq units) of the region
A={(x,y):y22≤x≤y+4} isView SolutionIf the area (in sq. units) of the region
{(x,y):y2≤4x,x+y≤1,x≥0,y≥0} is a√2+b, then a−b is equal to :View SolutionThe area (in sq units) of the region described by {(x,y):y2≤2xandy≥4x−1} is
View SolutionThe area (in square units) of the region bounded by y2=2xandy=4x−1 , is
View SolutionFind the area of the region {(x,y):y2≤4x,4x2+4y2≤9}
View SolutionThe area (in sq. units) of the region A={(x,y)∈R×R∣0≤x≤3,0≤y≤4,y≤x2+3x} is :
View Solution

