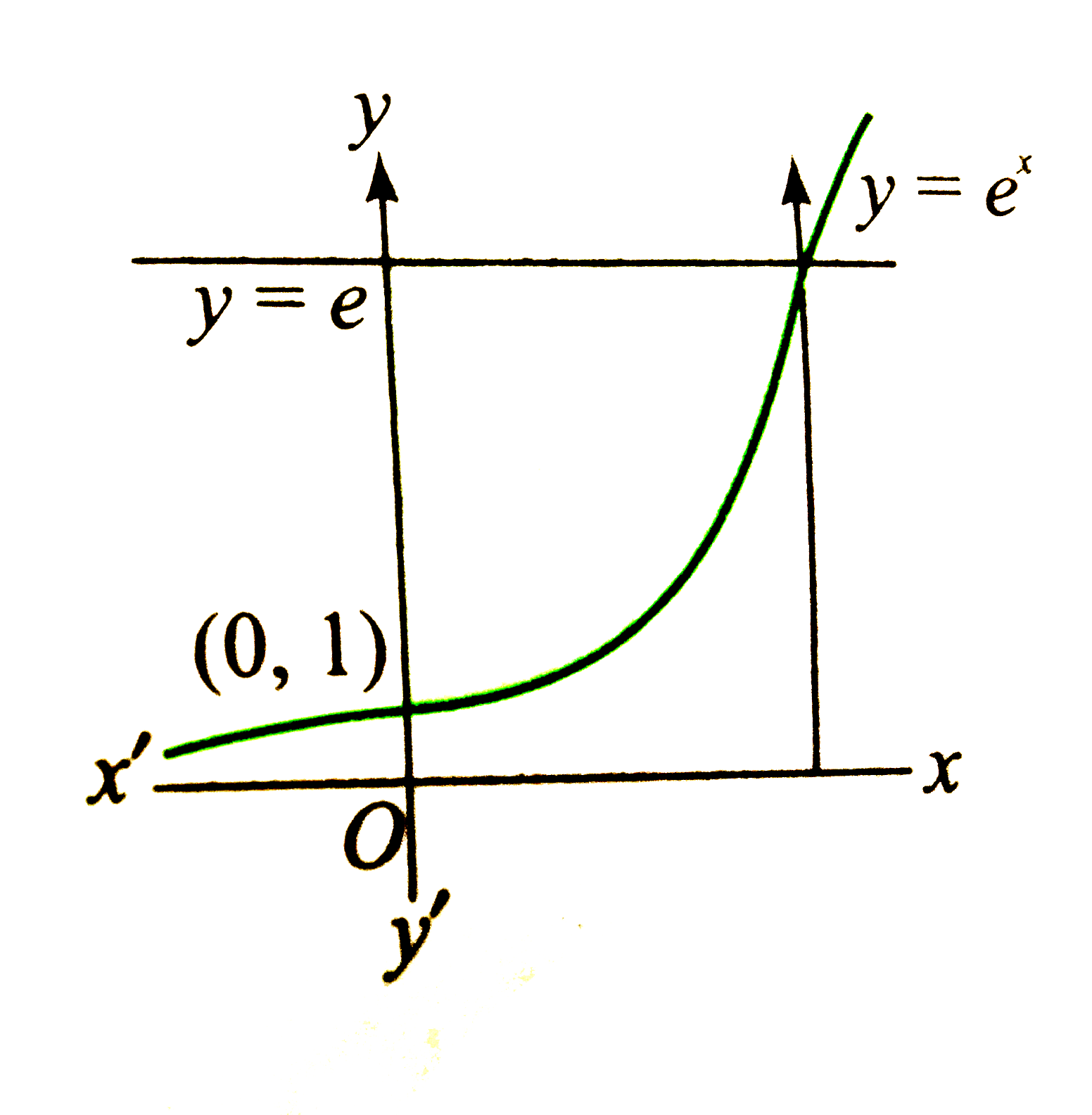
The area of the region bounded by the curve y=ex and lines x=0 and y=e is
e−1
e∫1 In (e+1−y)dy
e−1∫0exdx
e∫1 In y dy
The correct Answer is:B, C, D
Required area =e∫1 In ydy
=(y In y−y)e1
=(e−e)−{−1}
=1
Also,
e∫1 In ydye∫1 In (e+1−y)dy
Further Required area =e×1−1∫0exdx
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Linkded Comprehension Type21videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type5videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Exercises - Single Correct Answer Type40videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
Area of the region bounded by the curve y=tanx and lines y = 0 and x = 1 is
View SolutionThe area of the region bounded by the curve y=x3 , and the lines , y=8 and x=0, is
View SolutionThe area of the region bounded by the curve y=x2−2 and line y = 2 , is equal to
View SolutionFind the area of the region bounded by the curves y=x3 and the lines y=x+6 and y=0.
View SolutionA body weighs w Newton on the surface of the earth. Its weight at a height equal to half the radius of the earth, will be xyw where x and y are coprimes . Find x and y
View SolutionFind the area of the region bounded by the curve y=x3 and the lines y = x + 6 and y =0.
View SolutionThe area of the region bounded by the curve x=2y+3 and the lines y=1,y=−1 is
View SolutionFind the area of the region bounded by the curve y2=xand the lines x=1,x=4and the x-axis.
View SolutionThe area of the region bounded by the curve y = x + 1 and the lines x=2,x=3, is
View SolutionThe area of the region bounded by the curve y=xsinx, x-axis, x=0 and x=2π is :
View Solution
