The area of the region bounded by the ellipse , is …….. sq. units.
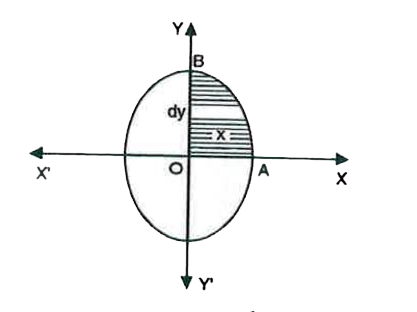
To find the area of the region bounded by the ellipse given by the equation
x264+y2100=1,
we can follow these steps:
Step 1: Identify the semi-major and semi-minor axes
The standard form of the ellipse equation is
x2a2+y2b2=1,
where a2=64 and b2=100.
Calculating a and b:
a=√64=8,b=√100=10.
Here, a<b, meaning the semi-major axis is along the y-axis and the semi-minor axis is along the x-axis.
Step 2: Calculate the area of the ellipse
The area A of an ellipse is given by the formula:
A=π⋅a⋅b.
Substituting the values of a and b:
A=π⋅8⋅10=80π.
Step 3: State the final answer
Thus, the area of the region bounded by the ellipse is
80π square units.
---
The standard form of the ellipse equation is
The area A of an ellipse is given by the formula:
Thus, the area of the region bounded by the ellipse is
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - DIFFERENTIAL EQUATIONS
38 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - PROBABILITY DISTIBUTIONS
39 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - DEFINITE INTEGRATION
59 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
Knowledge Check
The area of the region bounded by the ellipse x225+y216=1 is
A20π sq unitsB20π2 sq unitsC16π2 sq unitsD25π sq unitsThe area of the region bounded by the ellipse x225+y216=1 is
A20π sq unitsB20π2 sq unitsC16π2 sq unitsD25π sq unitsThe area bounded by the ellipse x24+y225=1 is
A2πsq.unitsB5πsq.unitsC20πsq.unitsD10πsq.units
The area of the region bounded by the curves x2+y2=8andy2=2x (in sq. unit) is
View SolutionFind the area of the region bounded by the ellipse x24+y29=1.
View SolutionFind the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.
View SolutionFind the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.
View SolutionThe area of the region bounded by the curves y=x3,y=1x,x=2 and x - axis (in sq. units) is
View Solution
