The base of an isosceles triangle measures 4 units base angle is equal to $45^{\circ}$ . A straight line cuts the extension of the base at a point M at the angle $θ$ and bisects the lateral side of the triangle which is nearest to M.
The possible range of values in which area of quadrilateral which straight line cuts off from the given triangle lie in

A

$(\frac{5}{2}, \frac{7}{2})$

B

(4,3)

C

(4,5)

D

(3,4)

Text Solution

Verified by Experts

The correct Answer is:D

For the given specification of the triangle, consider triangle ABC as shown in the figure.

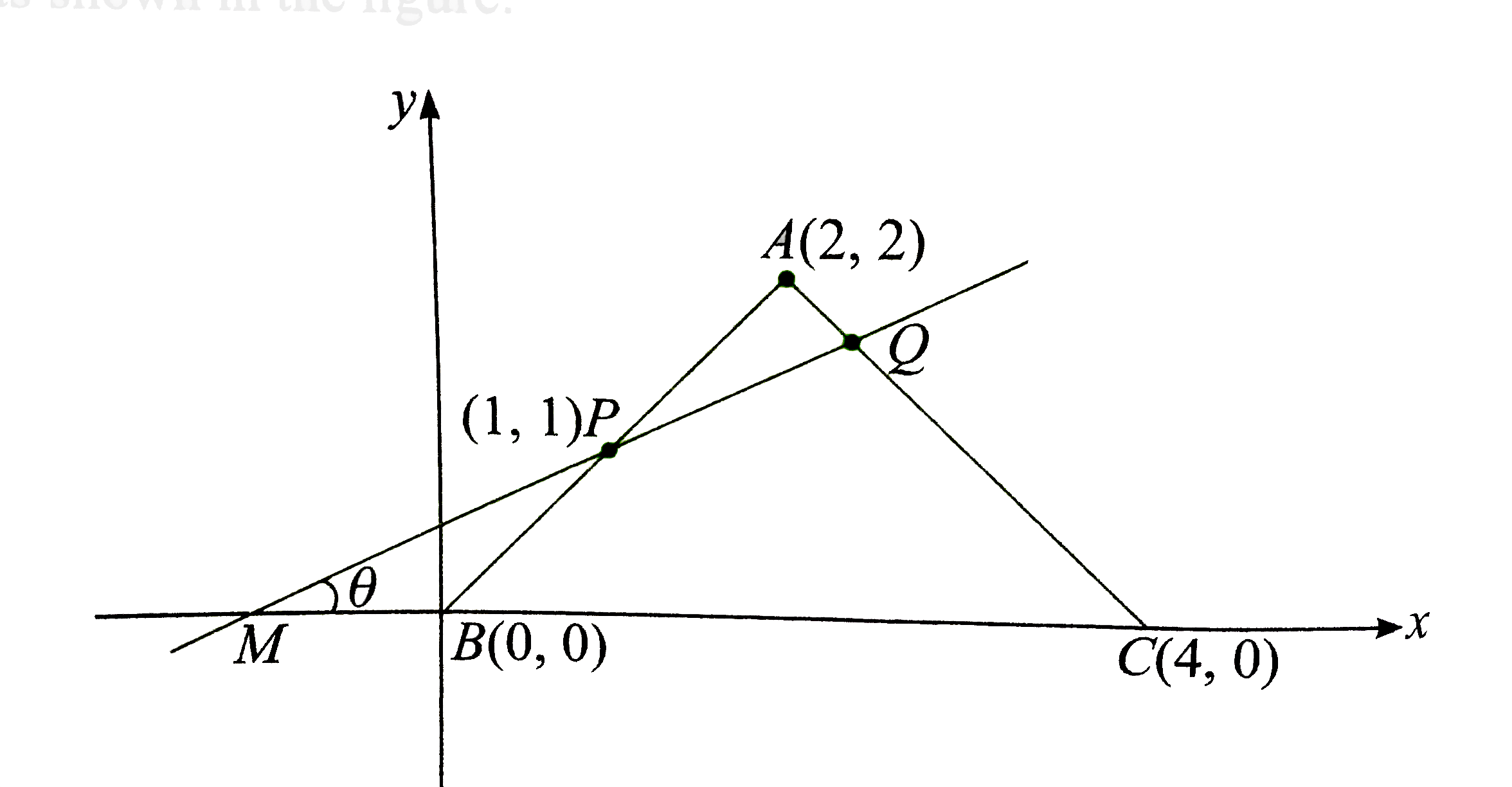
Equation of line PM is
$y - 1 = tan θ (x - 1)$
For point Q, solving MP and AC,
$4 - x - 1 = tan θ (x - 1)$
$\Rightarrow Q \equiv (\frac{3 + tan θ}{1 + tan θ}, \frac{1 + 3 tan θ}{1 + tan θ})$
$Area of Δ A P Q = \frac{1}{2} | | \begin{matrix} 1 & 1 & 1 \\ 2 & 2 & 1 \\ \frac{3 + tan θ}{1 + tan θ} & \frac{1 + 3 tan θ}{1 + tan θ} & 1 \end{matrix} | | = \frac{1 - tan θ}{1 + tan θ} (As θ < π / 4)$
Area of quadilateral BPQC,
$Δ = \frac{1}{2} \times 4 \times 2 - (\frac{1 - tan θ}{1 + tan θ})$
$or Δ = (\frac{3 + 5 tan θ}{1 + tan θ})$
$or Δ = 5 - \frac{2}{1 + tan θ} where θ \in (0, \frac{π}{4})$
$∴ Δ \in (3, 4)$
${(P Q)}^{2} = {(\frac{3 + tan θ}{1 + tan θ} - 1)}^{2} + {(\frac{1 + 3 tan θ}{1 + tan θ} - 1)}^{2}$
$= \frac{4 (1 + {tan}^{2} θ)}{1 + {tan}^{2} θ + 2 tan θ}$
$= \frac{4}{1 + \frac{2 tan θ}{1 + {tan}^{2} θ}}$
$= \frac{4}{1 + sin 2 θ}$
$S o, {(P Q)}^{2} \in (2, 4)$
$∴ P Q \in (\sqrt{2}, 2)$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The base of an isosceles triangle measures 4 units base angle is equal to $45^{\circ}$ . A straight line cuts the extension of the base at a point M at the angle $θ$ and bisects the lateral side of the triangle which is nearest to M.
The area of quadrilateral which the straight line cuts off from the given triangle is
A $\frac{3 + tan θ}{1 + tan θ}$
B $\frac{3 + 5 tan θ}{1 + tan θ}$
C $\frac{3 + tan θ}{1 - tan θ}$
D $\frac{3 + 2 tan θ}{1 + tan θ}$
Question 2 - Select One
The base of an isosceles triangle measures 4 units base angle is equal to $45^{\circ}$ . A straight line cuts the extension of the base at a point M at the angle $θ$ and bisects the lateral side of the triangle which is nearest to M.
The length of portion of straight line inside the triangle may lie in the range
A(2,4)
B $(\frac{3}{2}, \sqrt{3})$
C $(\sqrt{2}, 2)$
D $(\sqrt{2}, \sqrt{3})$
Question 3 - Select One
In an isosceles triangle with base angle $α$ and lateral side 4, Rr=
A $8 cos α$
B $\frac{8 cos α}{1 - cos α}$
C $\frac{8 cos α}{1 + cos α}$
D $8 cos α - (1 - cos α)$

CENGAGE-STRAIGHT LINES-Exercise (Comprehension)

Home
Ask Doubt
Profile