The circle inscribed in the triangle ABC touches the side BC, CA and AB in the point A1B1andC1 respectively. Similarly the circle inscribed in the ΔA1B1C1 touches the sieds in A2,B2,C2 respectively and so on. If AnBnCn be the nth Δ so formed, prove that its angle are
π3−(2)−n(A−π3),π3−(2)−n(B−π3),π3−(2)−n(C−π3). Hence prove that the triangle so formed is ultimately equilateral. Solution in Punjabi
The correct Answer is:An=Bn=Cn=π3.
Step by step video & image solution for The circle inscribed in the triangle ABC touches the side BC, CA and AB in the point A_(1)B_(1) and C_(1) respectively. Similarly the circle inscribed in the Delta A_(1) B_(1) C_(1) touches the sieds in A_(2), B_(2), C_(2) respectively and so on. If A_(n) B_(n) C_(n) be the nth Delta so formed, prove that its angle are pi/3-(2)^-n(A-(pi)/(3)), pi/3-(2)^-n(B-(pi)/(3)),pi/3-(2)^-n(C-(pi)/(3)). Hence prove that the triangle so formed is ultimately equilateral. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Match the statements of Column I with values of Column II.

View SolutionIn the given figure,if AB=AC,∠BAD=30∘andAE=AD, then x is equal to
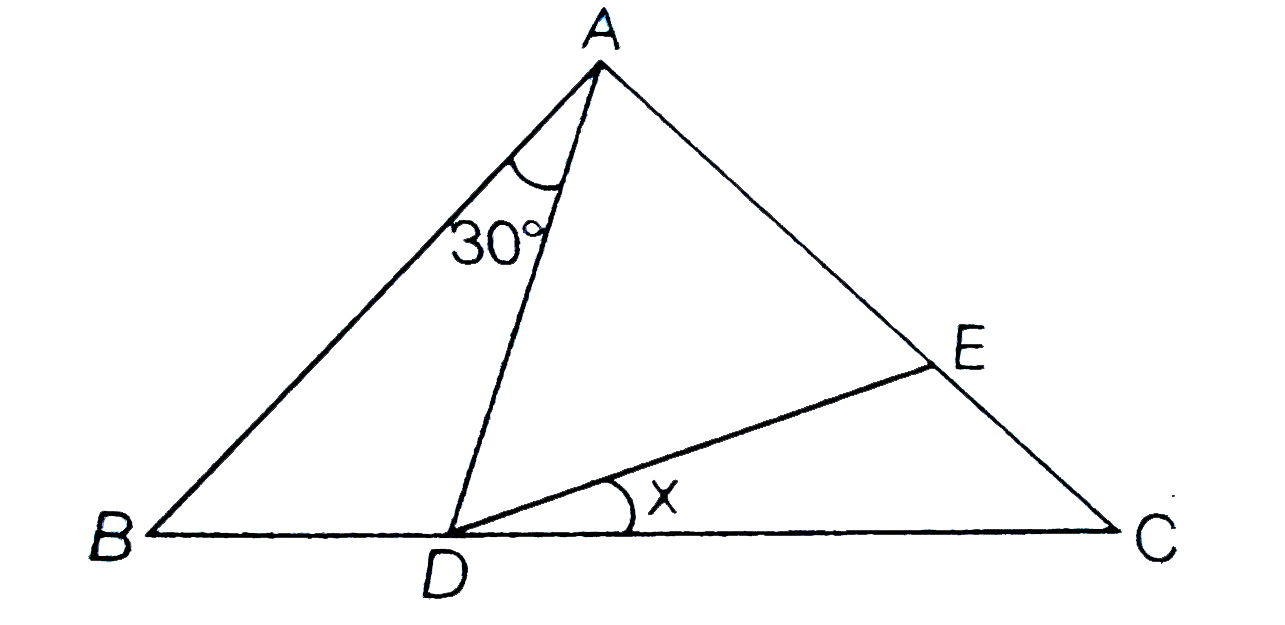
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View Solutionif Delta=det[[a_(1),b_(1),c_(1)a_(2),b_(2),c_(2)a_(3),b_(3),c_(3)]]
View SolutionLet An=a1+a2+……+an,Bn=b1+b2+b3+….+bn,Dn=c1+c2+…..+cn and cn=a1bn+a2bn−1+…….+anb1Aan∈N. Using mathematical induction , prove that
(a) Dn=a1Bn+a2Bn−1+.....+anB1=b1An+b2An−1+......+bnA1∀n∈N
(b) D1+D2+......+Dn=A1Bn+A2Bn−1+.....+AnB1∀n∈N
View SolutionIf ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=5, then the value of
Δ=∣∣ ∣∣b2c3−b3c2a3c2−a2c3a2b3−a3b2b3c1−b1c3a1c3−a3c1a3b1−a1b3b1c2−b2c1a2c1−a1c2a1b2−a2b1∣∣ ∣∣ is
View Solutionif A1,B1,C1……. are respectively the cofactors of the elements a1,b1,c1…… of the determinant
Δ=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣,Δ≠0 then the value of ∣∣∣B2C2B3C3∣∣∣ is equal to
View SolutionStatement -1 Consider the determinant
Δ=∣∣ ∣ ∣∣a1+b1x2a1x2+b1c1a2+b2x2a2x2+b2c2a3+b3x2a3x2+b3c3∣∣ ∣ ∣∣=0,
where ai,bi,ci∈ R (i=1,2,3) and x∈ R
Stement -2 If ∣∣ ∣∣a1b2c3a2b2c2a3b3c3∣∣ ∣∣ =0, then Δ =0
View SolutionThe circle inscribed in the triangle ABC touches the side BC, CA and AB in the point A1B1andC1 respectively. Similarly the circle inscribed in the ΔA1B1C1 touches the sieds in A2,B2,C2 respectively and so on. If AnBnCn be the nth Δ so formed, prove that its angle are
(C−π3). Hence prove that the triangle so formed is ultimately equilateral.
View SolutionIf ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=Δ, then ∣∣ ∣∣A1B1C1A2B2C2A3B3C3∣∣ ∣∣=
View Solutionयदि सारणिक Δ=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣ में A1,B1,C1,.... आदि क्रमश: अवयव a1,b1,c1,.... आदि के सहखण्ड हो, तो सिद्ध कीजिए कि Δ2=∣∣ ∣∣A1B1C1A2B2C2A3B3C3∣∣ ∣∣
View SolutionIf Ai,Bi,Ci are the cofactors of ai,bi,ci respectively,i=1,2,3 in Δ=∣∣ ∣∣a1b2c1a2b2c2a3b3c3∣∣ ∣∣show that ∣∣ ∣∣A1B1C1A2B2C2A3B3C3∣∣ ∣∣=Δ0
View Solutionयदि Δ=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣ और A1,B1,C1 आदि क्रमशः a1,b1,c1 आदि के सहखण्डज हो, तो सारणिक ∣∣ ∣∣A1B1C1A2B2C2A3B3C3∣∣ ∣∣ का मान है
View Solutionमाना तीन अशून्य सदिश a=a1i+a2j+a3k,b=b1i+b2j+b3k व c=c1i+c2j+c3k हैं |
यदि c एक इकाई सदिश है जो a तथा b पर लम्ब है एवं a व b के बीच का कोण π6 हो, तो ∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣2=
View Solutionयदि Δ=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣ और A1,B1,C1 आदि क्रमशः a1,b1,c1 आदि के सहखण्डज हो, तो सारणिक ∣∣ ∣∣A1B1C1A2B2C2A3B3C3∣∣ ∣∣ का मान है
View Solution
