The circle x2+y2−6x−10y+k=0 does not touch or intersect the coordinate axes, and the point (1, 4) is inside the circle. Find the range of value of k.
The equation of the circle is
x2+y2−6x−10y+k=0 (1)
whose center is C(3,5) and radius
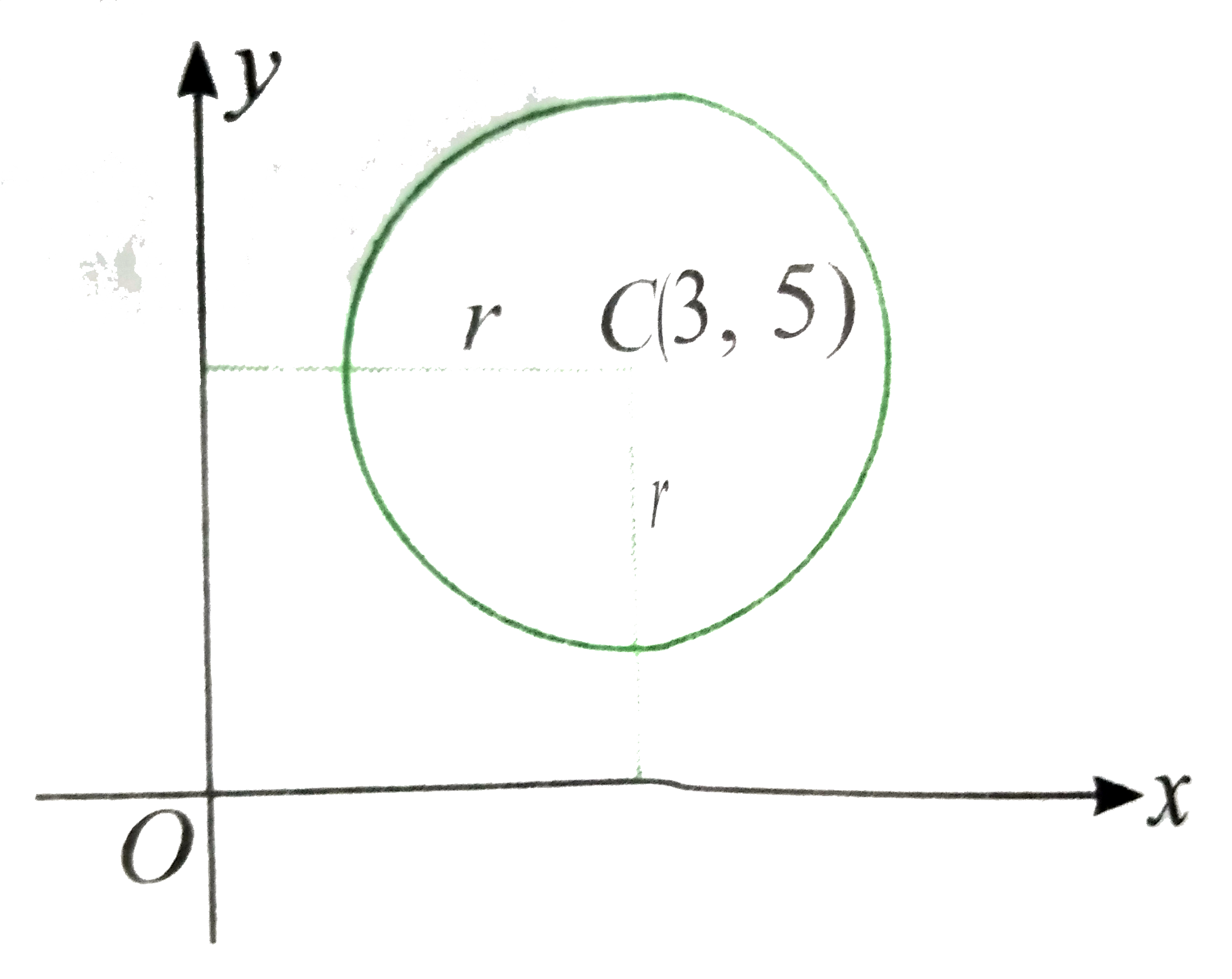
r=√34−k
If the circle does not touch or intersect the x-axis, then radius
r<y coordinate of center C
or √34−k<5
or 34−k<25
or k>9 (2)
Also, if the circle does not touch or intersect the y-axis, then the radius
r<x− coordinate of center C
or √34−k<3
or 34−k<9
or k>25 (3)
If the point (1,4) is inside the circle, then
Its distance from center C<r
or √(3−2)2+(5−4)2<√34−k
or 5<34−k
or k<29 (4)
Now, all the conditions (2),(3), and (4) are satisfied if 25<k<29 which is the required range of the values of k.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Examples
13 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
(i) Prove that the line y = 2x touches the circle x2+y2+16x+12y4−80=0 and find the co-ordinates of the point of contact.
(ii) The circle x2+y2−6x−10y+y=0 does not intersect or touch either axis and the point (1,4) is inside the circle. Calculate the range of possible values of p .
View SolutionShow that the circle x2+y2−2ax−2ay+a2=0 touches both the coordinate axes.
View SolutionIf the lines 2x+3y+1=0,6x+4y+1=0 intersect the co-ordinate axes in 4 points, then the circle passing through the points is
View SolutionA circle touches both the coordinate axes and the line x−y=√2a,a>0, the coordinates of the centre of the circle cannot be
View SolutionShow that the circle x2+y2−4x+4y+4=0 touches the co-ordinate axes. If the points of contact are A and B, find the equation of the circle which passes through A, B and the origin,
View SolutionFind the equation of the circle which touches the coordinate axes and whose centre lies on the line x−2y=3.
View SolutionTangent drawn from the point P(4,0) to the circle x2+y2=8 touches it at the point A in the first quadrant. Find the coordinates of another point B on the circle such that AB=4 .
View SolutionThe circle x2+y2−4x−4y+4=0 is inscribed in a triangle which has two of its sides along the coordinate axes. The locus of the circumcenter of the triangle is x+y−xy+k(x2+y2)12=0 . Find k.
View SolutionShow that the circles x2+y2−10x+4y−20=0 and x2+y2+14x−6y+22=0 touch each other. Find the coordinates of the point of contact and the equation of the common tangent at the point of contact.
View SolutionFind the equation of the circle which touches the coordinate axes and whose centre lies on the line x-2y = 3 .
View Solution
