The corner points of the feasible region of a system of linear inequalities are (0, 0), (4,0), (3,9), (1, 5) and (0, 3). If the maximum value of objective function, Z = ax + by occurs at points (3, 9) and (1, 5), then the relation between a and b is:
a-2b =0
2a-b=0
a + 2b =0
2a +b=0
To find the relation between a and b given that the maximum value of the objective function Z=ax+by occurs at the points (3,9) and (1,5), we will follow these steps:
Step 1: Write the objective function for the given points
The objective function is given by:
Z=ax+by
For the point (3,9):
Z1=a(3)+b(9)=3a+9b
For the point (1,5):
Z2=a(1)+b(5)=a+5b
Step 2: Set the two expressions equal to each other
Since both points yield the maximum value of Z, we can set the two expressions equal:
3a+9b=a+5b
Step 3: Rearrange the equation
Rearranging the equation gives:
3a+9b−a−5b=0
(3a−a)+(9b−5b)=0
2a+4b=0
Step 4: Factor out common terms
Factoring out the common factor of 2:
2(a+2b)=0
Step 5: Solve for the relation between a and b
Since 2 is not zero, we can divide both sides by 2:
a+2b=0
Conclusion
Thus, the relation between a and b is:
a+2b=0
The objective function is given by:
Z=ax+by
Z1=a(3)+b(9)=3a+9b
Z2=a(1)+b(5)=a+5b
Since both points yield the maximum value of Z, we can set the two expressions equal:
3a+9b=a+5b
Rearranging the equation gives:
3a+9b−a−5b=0
(3a−a)+(9b−5b)=0
2a+4b=0
Factoring out the common factor of 2:
2(a+2b)=0
Since 2 is not zero, we can divide both sides by 2:
a+2b=0
Thus, the relation between a and b is:
a+2b=0
Topper's Solved these Questions
- SAMPLE PAPER 09BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 09EXERCISE - SECTIONS-B
19 Videos
- SAMPLE PAPER 09BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 09EXERCISE - SECTIONS-C
8 Videos
- SAMPLE PAPER - 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 5EXERCISE - Section - C
10 Videos
- SAMPLE PAPER 11 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 11 EXERCISE - SECTION- C
4 Videos
Similar Questions
The corner points of a feasible region determined by a system of linear inequations are (0,0),(4,0),(5,2),(2,2) and (0, 1). If the objective function is Z = x + y, then maximum of Z occurs at:
View SolutionThe corner points of a feasible region determined by a system of linear inequalities are (20,40),(50,100),(0,200) and (0,50). If the objective funtion Z=x+2y, then maximum of Z occurs at.
View Solution
Knowledge Check
The corner points of the feasible region of a system of linear inequations are (0, 0), (5, 0), (6,5), (6, 8), (4, 10) and (0,8). If Z = 3x - 4y, then the minimum value of Z occurs at:
A(0,8)B(6,5)C(6,8)D(4, 10)The corner points of the feasible region determined by a system of linear inequations are (0,0),(4,0),(2,4) and (0,5). If the minimum value of Z=ax+by,a, b>0 occurs at (2,4) and (0,5) ,then :
Aa=2bB2a=bCa=bD3a=bIf the corner points of a feasible region of system of linear inequalities are (15,20) (40,15) and (2,72) and the objective function is Z = 6x + 3y then Zmax−Zmin =
A135B78C57D101
The corner points of the feasible region of the system of linear inequations x+y≥2,x+y≤5,x−y≥0,x,y≥0 are :
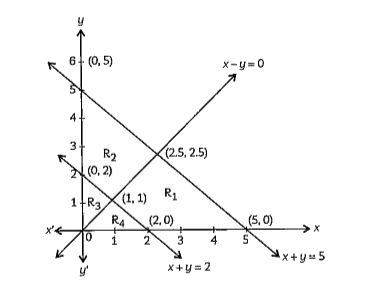
View SolutionThe corneer points of a feasible region, determined by a system of linear inequations, are (0,0),(1,0),(4,3),(2,1)and(0,1). If the objective function is Z=2x−3y, then the minimum value of Z is :
View Solutionthe corner points of the feasible region of a system of linear inequalities 3x+5y≤15,5x+2y≥10,x≥0,y≥0, are:
View SolutionThe corner points of the feasible region of an LPP are (0,0),(0,8),(2,7),(5,4) and (6,0). The maximum value of the objective function Z = 3x + 2y is:
View SolutionThe corner points of the feasible region of a LPP are (20,0),(10,50),(0,60) and (0,0). If Z= 50x +15y, then maximum value of Z occurs at :
View Solution
