The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If $∠ D A C = 32^{\circ} and ∠ A O B = 70^{\circ}$ , then $∠ D B C$ is equal to

A

$24^{\circ}$

B

$86^{\circ}$

C

$38^{\circ}$

D

$32^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Given, $∠ A O B = 70^{\circ} and ∠ D A C = 32^{\circ}$

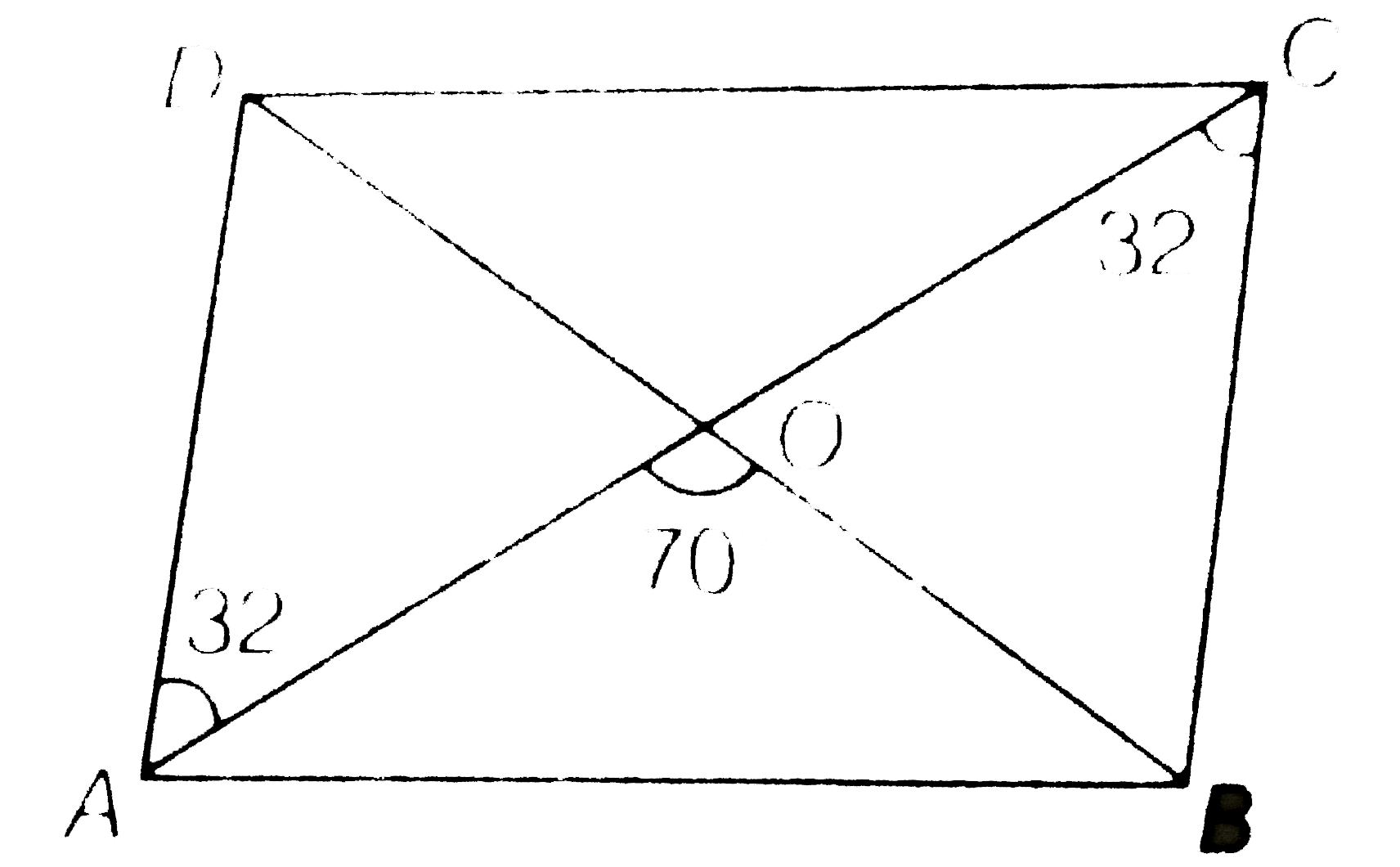
$∠ A C B = 32^{\circ} [A D ∣ ∣ B C and A C$ is transversal]
Now, $∠ A O B + ∠ B O C = 180^{\circ}$ [linear pair axiom]
$\Rightarrow ∠ B O C + ∠ B C O + ∠ O B C = 180^{\circ}$ [by angle sum property of a triangle]
$\Rightarrow 110^{\circ} + 32^{\circ} + ∠ O B C = 180^{\circ} [∵ ∠ B C O = ∠ A C B = 32^{\circ}]$
$\Rightarrow ∠ O B C = 180^{\circ} - (110^{\circ} + 32^{\circ}) = 38^{\circ}$
$∴ ∠ D B C = ∠ O B C = 38^{\circ}$

|

Updated on:21/07/2023

Class 9 MATHS QUADRILATERALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The diagonals $A C$ and $B D$ of a parallelogram $A B C D$ intersect each other at the point O. If $∠ D A C = 32^{\circ} and ∠ A O B = 70^{\circ}, find ∠ D B C .$
A $35^{\circ}$
B $38^{\circ}$
C $40^{\circ}$
D $45^{\circ}$
Question 2 - Select One
The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that
AAP. CP = BP. DP
BAP.BP = CP. DP
CAP. CD = AB. CP
DBP. AB = CD.CP
Question 3 - Select One
The diagonals AC and BD of a cyclic quadrilateral ABCD inter sect each other at the point P. Then, it is always true that
A(a) $B P . A B = C D . C P$
B(b) $A P . C P = B P . D P$
C(c) $A P . B P = C P . D P$
D(d) $A P . C D = A B . C P$

NCERT EXEMPLAR-QUADRILATERALS -Quadrilaterals

Home
Ask Doubt
Profile