Question

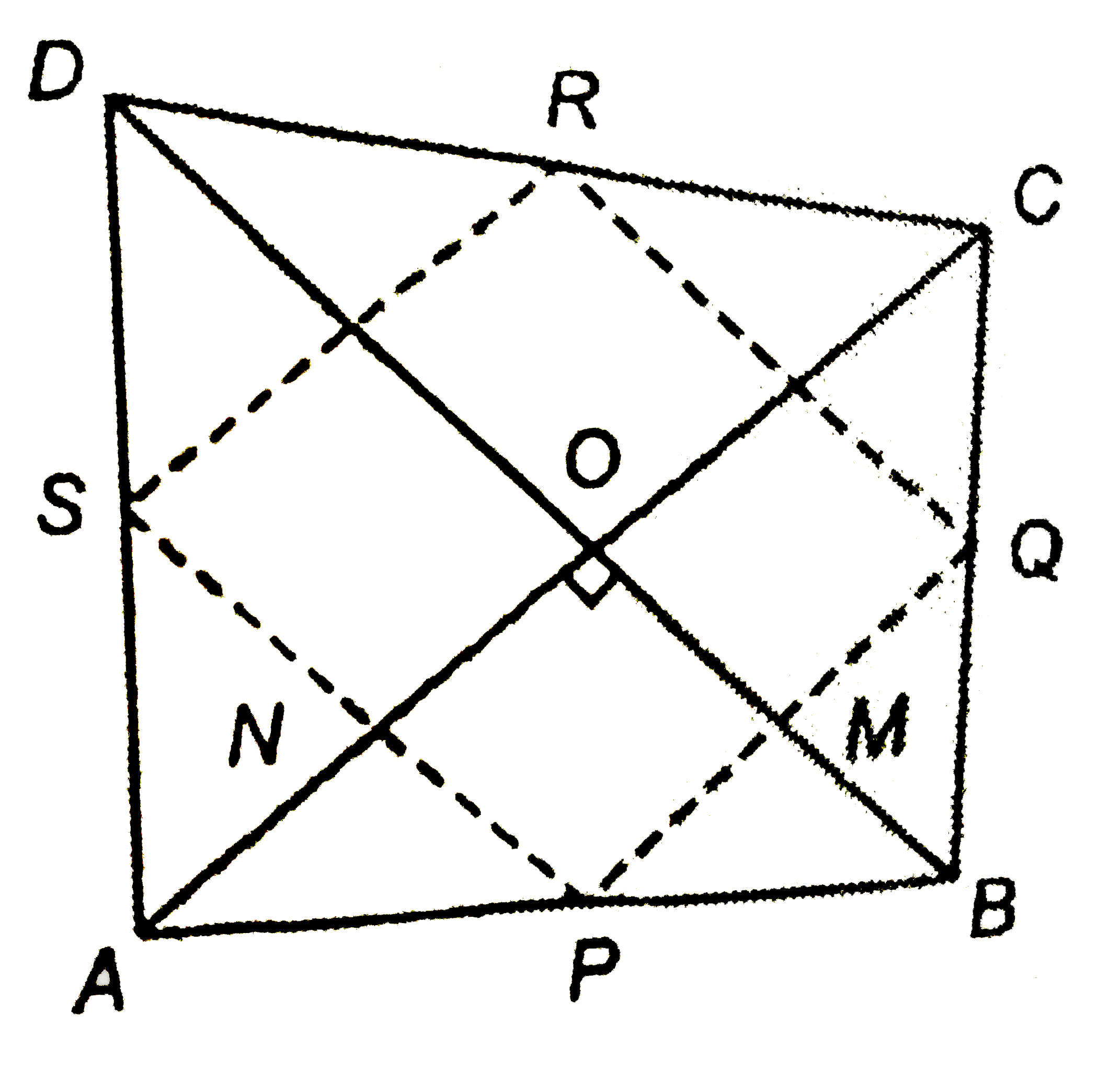
The diagonals of a quadrilateral $ABCD$
are perpendicular. Show that the quadrilateral, formed by joining the
mid-points of its sides, is a rectangle.

Explanation

To prove that the quadrilateral formed by joining the midpoints of the sides of quadrilateral ABCD (where the diagonals AC and BD are perpendicular) is a rectangle, we will follow these steps:

Step 1: Identify the Midpoints
Let P, Q, R, and S be the midpoints of sides AB, BC, CD, and DA respectively.

Step 2: Prove PQ is Parallel to SR
In triangle ABC, since P is the midpoint of AB and Q is the midpoint of BC, by the Midpoint Theorem, we have:
\( PQ \parallel AC \)
and
\( PQ = \frac{1}{2} AC \)

In triangle ACD, since S is the midpoint of AD and R is the midpoint of CD, we also have:
\( SR \parallel AC \)
and
\( SR = \frac{1}{2} AC \)

Since both PQ and SR are parallel to AC and equal in length, we conclude:
\( PQ \parallel SR \quad \text{and} \quad PQ = SR \)

Step 3: Prove PS is Parallel to QR
Now, consider triangle ABD. Since P is the midpoint of AB and S is the midpoint of AD, by the Midpoint Theorem:
\( PS \parallel BD \)
and
\( PS = \frac{1}{2} BD \)

In triangle BCD, since Q is the midpoint of BC and R is the midpoint of CD, we have:
\( QR \parallel BD \)
and
\( QR = \frac{1}{2} BD \)

Since both PS and QR are parallel to BD and equal in length, we conclude:
\( PS \parallel QR \quad \text{and} \quad PS = QR \)

Step 4: Conclude that PQRS is a Parallelogram
Since we have shown that:
1. \( PQ \parallel SR \) and \( PQ = SR \)
2. \( PS \parallel QR \) and \( PS = QR \)

This means that quadrilateral PQRS is a parallelogram.

Step 5: Show that One Angle is 90 Degrees
Now, we need to show that one angle of the parallelogram PQRS is 90 degrees. Since diagonals AC and BD of quadrilateral ABCD are perpendicular, we have:
\( \angle APB = 90^\circ \)
This means that:
\( \angle SPQ = \angle APB = 90^\circ \)

Step 6: Conclude that PQRS is a Rectangle
Since PQRS is a parallelogram and one of its angles (angle SPQ) is 90 degrees, it follows that all angles in the parallelogram are 90 degrees. Therefore, PQRS is a rectangle.

Thus, we have shown that the quadrilateral formed by joining the midpoints of the sides of quadrilateral ABCD is a rectangle.