The equation of the perpendicular bisector of line is and the co-ordinates of point are . Co-ordinates of are :
The correct Answer is:C
Step by step video & image solution for The equation of the perpendicular bisector of line AB is x+2y=8 and the co-ordinates of point A are (1,1). Co-ordinates of B are : by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise207videos
STRAIGHT LINES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE7videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE10videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
The line x-4y =6 is the perpendicular bisector of the line segment AB. If B= (1, 3), find the co-ordinates of point A.
View SolutionGiven equation of line L1 is y=4
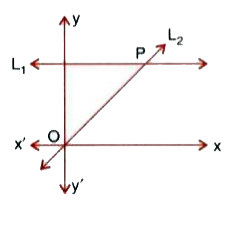
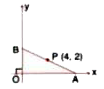
Write the co-ordinates of point P.View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
 View Solution
View SolutionThe co-ordinates of the mid-point of line joining the points A and B are (2, -3). If the co-ordinates of point A are (-3, 4), then find the co- ordinates of point B.
View SolutionA point P is reflected in the x - axis . Co - ordinates of its image are (8,-6).
Find the co - ordinates of P.View SolutionThe co-ordinates of two vertices of ΔABC are A(-5,7,3) and B(7,-6,-1). The co-ordinates of its centroid are (1,1,1). Find the co-ordinates of vertex C.
View SolutionFind the co-ordinates of the point Q on x-axis which lies on the perpendicular bisector of the line segment joining the points A(-5.-2) and B(4.-2). Name the type of the triangle QAB.
View SolutionThe co-ordinates of the vertex A of a square ABCD are (1, 2) and the equation of the diagonal BD is x+2y=10. Find the equation of the other diagonal and the co-ordinates of the centre of the square.
View SolutionGiven M is the mid-point of AB, find the co-ordinates of:
B, if A = (3,-1) and M = (-1, 3).View SolutionThe point on the curve xy2=1 nearest to origin is_________. {Determine the co-ordinates of the point.}
View Solution
