Given M is the mid-point of AB, find the co-ordinates of:
B, if A = (3,-1) and M = (-1, 3).
To find the coordinates of point B given that M is the midpoint of segment AB, we can use the midpoint formula. The coordinates of point A are given as A = (3, -1) and the coordinates of the midpoint M are given as M = (-1, 3).
1. Understand the Midpoint Formula:
The midpoint M of a line segment AB, where A has coordinates (x1, y1) and B has coordinates (x2, y2), is given by:
M=(x1+x22,y1+y22)
2. Assign Known Values:
Here, we know:
- A = (3, -1) → x1 = 3, y1 = -1
- M = (-1, 3) → x = -1, y = 3
- We need to find B = (x2, y2).
3. Set Up the Equations:
From the midpoint formula, we can set up the following equations:
- For the x-coordinates:
−1=3+x22
- For the y-coordinates:
3=−1+y22
4. Solve for x2:
Multiply both sides of the first equation by 2:
−2=3+x2
Now, isolate x2:
x2=−2−3=−5
5. Solve for y2:
Multiply both sides of the second equation by 2:
6=−1+y2
Now, isolate y2:
y2=6+1=7
6. Final Coordinates of B:
Therefore, the coordinates of point B are:
B=(−5,7)
Summary:
The coordinates of point B are (-5, 7).
The midpoint M of a line segment AB, where A has coordinates (x1, y1) and B has coordinates (x2, y2), is given by:
M=(x1+x22,y1+y22)
Here, we know:
- A = (3, -1) → x1 = 3, y1 = -1
- M = (-1, 3) → x = -1, y = 3
- We need to find B = (x2, y2).
From the midpoint formula, we can set up the following equations:
- For the x-coordinates:
−1=3+x22
- For the y-coordinates:
3=−1+y22
Multiply both sides of the first equation by 2:
−2=3+x2
Now, isolate x2:
x2=−2−3=−5
Multiply both sides of the second equation by 2:
6=−1+y2
Now, isolate y2:
y2=6+1=7
Therefore, the coordinates of point B are:
B=(−5,7)
The coordinates of point B are (-5, 7).
Topper's Solved these Questions
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - EXERCISE 13 (C)
28 Videos
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - QUESTIONS
17 Videos
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - QUESTIONS
17 Videos
- SAMPLE PAPER 5 (MATHEMATICS)BOOK - ICSECHAPTER - SAMPLE PAPER 5 (MATHEMATICS)EXERCISE - SECTION C
8 Videos
- SHARES AND DIVIDENDSBOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )
20 Videos
Similar Questions
Given M is the mid-point of AB, find the co-ordinates of:
A, if M = (1, 7) and B = (-5, 10),
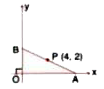
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the

co-ordinates of A and B.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
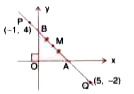
The co-ordinates of A and B.
View SolutionA straight line passes through the points P(−1,4) and Q(5,−2). It intersects x-axis at point A and y-axis at point B. M is the midpoint of the line segment AB. Find :
the co-ordinates of point M.
View SolutionFind the co-ordinates of the mid-point of the line segment joining the points A(3,−5)andB(1,1).
View SolutionA (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show
that : LM=12BC.
View SolutionIn the adjoining figure
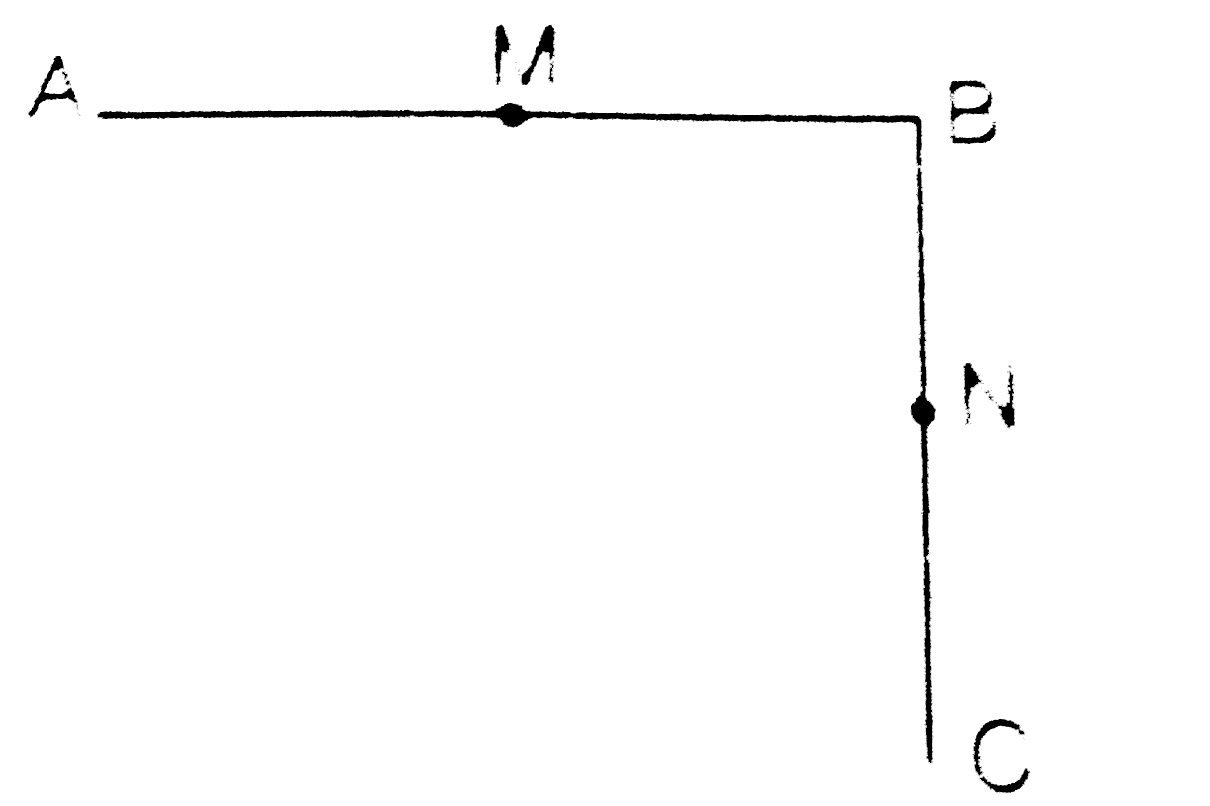
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
View SolutionThe line 4x + 5y + 20 = 0 meets x-axis at point A and y-axis at point B Find :
the co-ordinates of point P in AB such that AB : BP = 5:3.
View SolutionGravitational field in x−y plane is given as
E=(2xˆi+3y2ˆj)N/kg
Find difference in gravitation potential between two points A and B, where
co-ordinates of A and B are (2m,4m)and(6m,0).
View Solution
