Question

The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only, if

Options

A. ABCD is a rhombus
B. diagnols of ABCD are equal
C. diagonals of ABCD are equal and perpendicular
D. diagonals of ABCD are perpendicular

Answer

C

Explanation

Given, ABCD is a quadrilateral and P, Q, R and S are the mid-points of sides of AB, BC, CD and DA, respectively. Then, PQRS is square.
`therefore" "PQ=QR=RS=PS" "...(i)`
and `" "` PR=SQ
But `" "` PR=BC and SQ = AB
`therefore" "AB=BC`
Thus, all the sides of quadrilateral ABCD are equal.

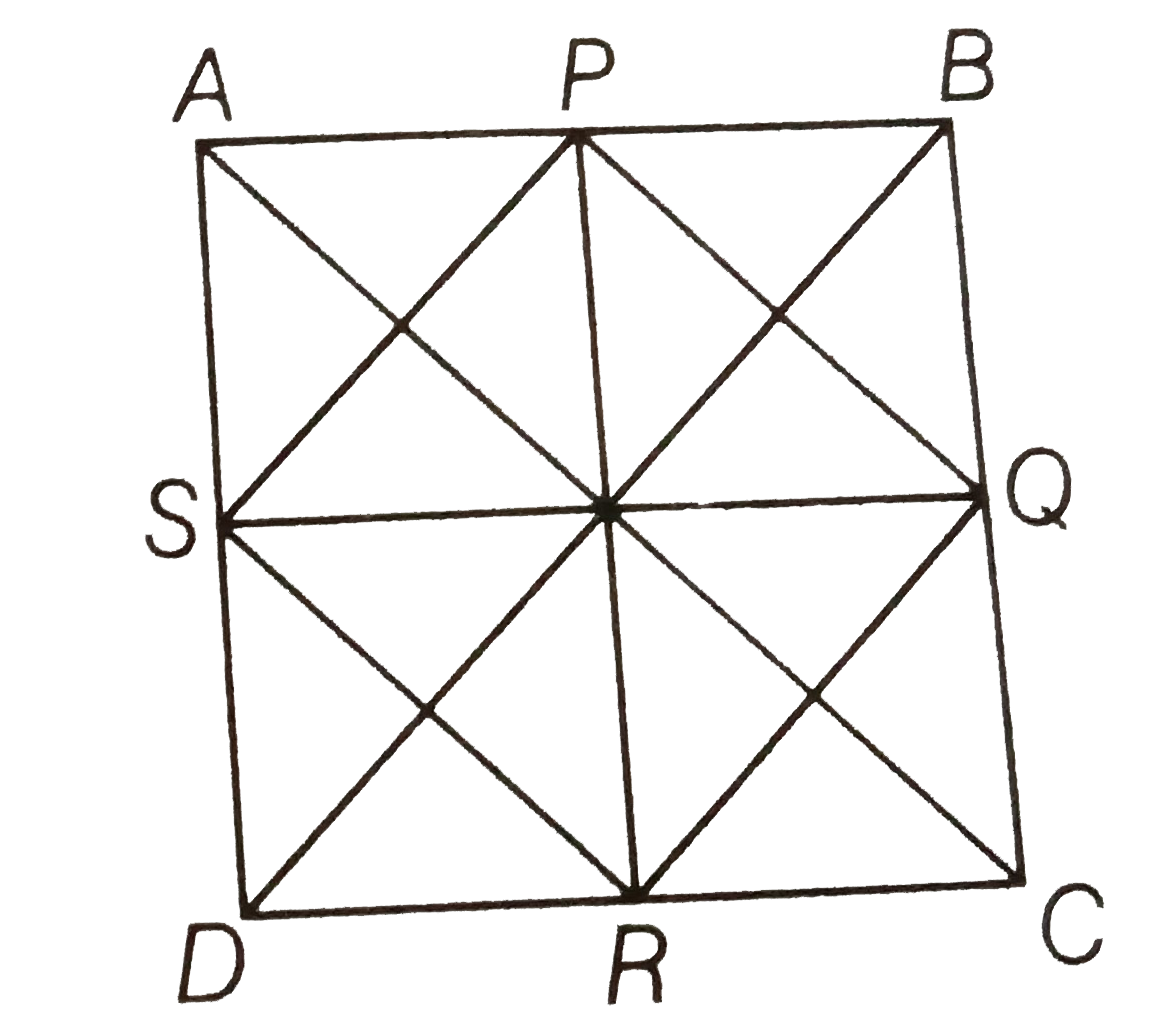
Hence, quadrilateral ABCD is either a square or a rhombus.
Now, in `Delta`ADB, use mid-point theorem
`SP||DB`
and `" "SP=(1)/(2)DB" "...(ii)`
Similarly in `Delta`ABC (by mid-point theorem) `PQ||AC and PQ = (1)/(2)AC" "...(iii)`
From Eq. (i), " " PS=PQ
`rArr" "(1)/(2)DB=(1)/(2)AC" "` [from Eqs. (ii) and (iii)]
`rArr" "DB=AC`
Thus, diagonals of ABCD are equal and therefore quadrilateral ABCD is a square not rhombus. So, diagonals of quadrilateral are also perpendicualar.