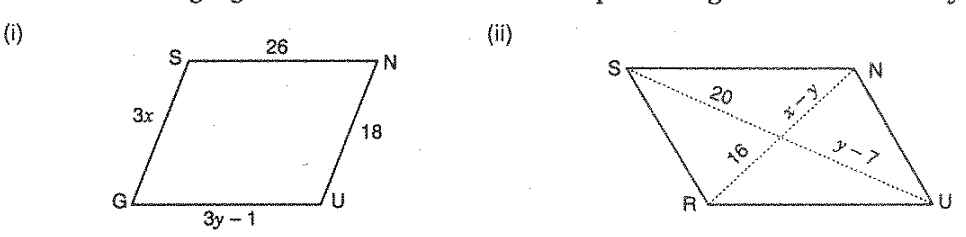
The following figures GUNS and RUNS are parallelograms.Find x and y. (Lengths are in cm)
To solve for x and y in the parallelograms GUNS and RUNS, we will use the properties of parallelograms, specifically that opposite sides are equal and that the diagonals bisect each other.
1. Identify the properties of the parallelogram:
In a parallelogram, opposite sides are equal in length.
2. Set up equations for the first parallelogram (GUNS):
- From the figure, we have one side represented as 3x and the opposite side as 18.
- Therefore, we can set up the equation:
3x=18
3. Solve for x:
- Divide both sides of the equation by 3:
x=183=6 cm
4. Set up equations for the first figure to find y:
- Another side is given as 3y−1 and is equal to 26.
- Set up the equation:
3y−1=26
5. Solve for y:
- First, add 1 to both sides:
3y=26+1=27
- Now, divide both sides by 3:
y=273=9 cm
6. Now, move to the second parallelogram (RUNS):
- The diagonals bisect each other, so we can set up the first equation:
x+y=16(1)
7. Set up another equation for y:
- One side is given as y+7 and is equal to 20.
- Set up the equation:
y+7=20
8. Solve for y:
- Subtract 7 from both sides:
y=20−7=13 cm
9. Substitute y back into equation (1) to find x:
- Substitute y=13 into x+y=16:
x+13=16
- Now, subtract 13 from both sides:
x=16−13=3 cm
Final Results:
- For the first parallelogram GUNS: x=6 cm, y=9 cm.
- For the second parallelogram RUNS: x=3 cm, y=13 cm.
In a parallelogram, opposite sides are equal in length.
- From the figure, we have one side represented as 3x and the opposite side as 18.
- Therefore, we can set up the equation:
3x=18
- Divide both sides of the equation by 3:
x=183=6 cm
- Another side is given as 3y−1 and is equal to 26.
- Set up the equation:
3y−1=26
- First, add 1 to both sides:
3y=26+1=27
- Now, divide both sides by 3:
y=273=9 cm
- The diagonals bisect each other, so we can set up the first equation:
x+y=16(1)
- One side is given as y+7 and is equal to 20.
- Set up the equation:
y+7=20
- Subtract 7 from both sides:
y=20−7=13 cm
- Substitute y=13 into x+y=16:
x+13=16
- Now, subtract 13 from both sides:
x=16−13=3 cm
- For the first parallelogram GUNS: x=6 cm, y=9 cm.
- For the second parallelogram RUNS: x=3 cm, y=13 cm.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.12videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.26videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERTCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.19videos
SQUARES AND SQUARE ROOTS
- BOOK - NCERTCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.38videos
VISUALISING SOLID SHAPES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the following figure, ABCD and AEFG are two parallelograms. If ∠C=55∘ find ∠F.
 A65∘B75∘C85∘D55∘
A65∘B75∘C85∘D55∘
In the following figures RISK and CLUE are parallelograms. Find the measure of x.
 View Solution
View SolutionPQRS is parallelogram find x,y,z
View SolutionIn the following figure of a ship, ABDH and CEFG are two parallelograms. Find the value of x.
 View Solution
View SolutionIn the following figure ,ABCD is a parallelogram . Find the value of r .
 View Solution
View SolutionIn Figure, RICE is parallelogram. Find x, y, z.
 View Solution
View SolutionThe following figures are parallelograms. Find the degree values of the unknowns x, y, z
 View Solution
View SolutionIn the following figure, ABCD and PQRS are two parallelograms such that ∠D=120∘and∠Q=70∘. Find the value of x.
View Solution