The following is the distribution of height of students of a certain
class in a certain city:
Find the median height.
To find the median height from the given distribution of heights, we will follow these steps:
Step 1: Organize the Data
We have the following data:
| Height (in cms) | No. of students |
|------------------|-----------------|
| 160 - 162 | 15 |
| 163 - 165 | 118 |
| 166 - 168 | 142 |
| 169 - 171 | 127 |
| 172 - 174 | 18 |
Step 2: Convert to Inclusive Class Intervals
The given class intervals are exclusive, so we will convert them to inclusive class intervals:
| Height (in cms) | No. of students |
|------------------|-----------------|
| 159.5 - 162.5 | 15 |
| 162.5 - 165.5 | 118 |
| 165.5 - 168.5 | 142 |
| 168.5 - 171.5 | 127 |
| 171.5 - 174.5 | 18 |
Step 3: Calculate Cumulative Frequency
Now we will calculate the cumulative frequency:
| Height (in cms) | No. of students | Cumulative Frequency |
|------------------|-----------------|----------------------|
| 159.5 - 162.5 | 15 | 15 |
| 162.5 - 165.5 | 118 | 15 + 118 = 133 |
| 165.5 - 168.5 | 142 | 133 + 142 = 275 |
| 168.5 - 171.5 | 127 | 275 + 127 = 402 |
| 171.5 - 174.5 | 18 | 402 + 18 = 420 |
Step 4: Find N and N/2
The total number of students (N) is the cumulative frequency of the last class, which is 420.
Now, calculate N/2:
N/2=420/2=210
Step 5: Identify the Median Class
We need to find the cumulative frequency just greater than N/2 (210). From the cumulative frequency table, we see that:
- The cumulative frequency of 165.5 - 168.5 is 275, which is the first cumulative frequency greater than 210.
Thus, the median class is 165.5 - 168.5.
Step 6: Identify Values for Median Formula
For the median class (165.5 - 168.5):
- Lower limit (L) = 165.5
- Frequency (f) = 142
- Cumulative frequency of the previous class (F) = 133
- Class width (H) = Upper limit - Lower limit = 168.5 - 165.5 = 3
Step 7: Apply the Median Formula
The formula for the median is:
Median=L+N/2−Ff×H
Substituting the values:
Median=165.5+210−133142×3
Median=165.5+77142×3
Median=165.5+231142
Median=165.5+1.63
Median≈167.13
Final Result
Hence, the median height is approximately 167.13 cm.
---
We have the following data:
|------------------|-----------------|
| 160 - 162 | 15 |
| 163 - 165 | 118 |
| 166 - 168 | 142 |
| 169 - 171 | 127 |
| 172 - 174 | 18 |
The given class intervals are exclusive, so we will convert them to inclusive class intervals:
|------------------|-----------------|
| 159.5 - 162.5 | 15 |
| 162.5 - 165.5 | 118 |
| 165.5 - 168.5 | 142 |
| 168.5 - 171.5 | 127 |
| 171.5 - 174.5 | 18 |
Now we will calculate the cumulative frequency:
|------------------|-----------------|----------------------|
| 159.5 - 162.5 | 15 | 15 |
| 162.5 - 165.5 | 118 | 15 + 118 = 133 |
| 165.5 - 168.5 | 142 | 133 + 142 = 275 |
| 168.5 - 171.5 | 127 | 275 + 127 = 402 |
| 171.5 - 174.5 | 18 | 402 + 18 = 420 |
The total number of students (N) is the cumulative frequency of the last class, which is 420.
N/2=420/2=210
We need to find the cumulative frequency just greater than N/2 (210). From the cumulative frequency table, we see that:
For the median class (165.5 - 168.5):
- Lower limit (L) = 165.5
- Frequency (f) = 142
- Cumulative frequency of the previous class (F) = 133
- Class width (H) = Upper limit - Lower limit = 168.5 - 165.5 = 3
The formula for the median is:
Median=L+N/2−Ff×H
Median=165.5+210−133142×3
Median=165.5+77142×3
Median=165.5+231142
Median=165.5+1.63
Median≈167.13
Hence, the median height is approximately 167.13 cm.
Topper's Solved these Questions
Similar Questions
The following is the distribution of height of students of a certain class in a certain city: Height (in cms): 160-162 163-165 166-168 169-171 172-174 No. of students: 15 118 142 127 18. Find the average height of maximum number of students.
View SolutionThe following distributions represent the height of 160 studens of a class :

Find the modal heightView SolutionThe heights (in cm) of 35 students of a class are given below :
Height (in cm)157152153154155156Number of students743597
Find the median height.View SolutionFind the unknown entries a,b,c,d,e and f in the following distribution of heights of students in a class
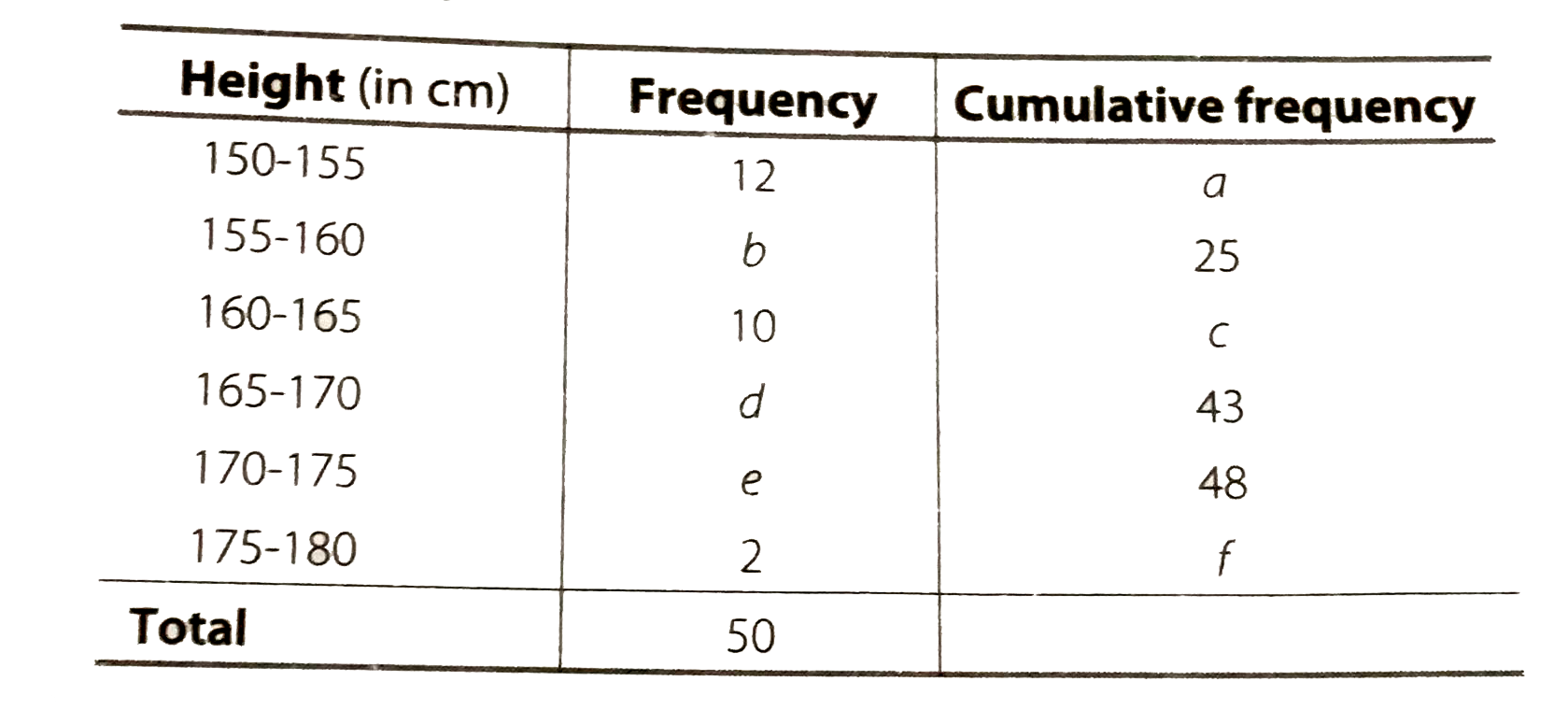 View Solution
View SolutionFind the unknown entries a,b,c,d,e and f in the following distribution of heights of students in a class
 View Solution
View SolutionThe following table shows the distribution of the heights of a group of factory workers :
Determine the cumulative frequencies
Ht. (cm): 150−155155−160160−165165−170170−175175−180180−185 No. of workers 6 12 18 20 13 8 6View SolutionThe following data give the distribution of heights of students :
Height(in cm)160150152161156154155Numbers of students12844337
The median of the distribution isView SolutionThe following data gives the distribution of height of students :
Height(in cm)160150152161156154155Numbers of students12844337
The median of the distribution isView SolutionFind the 20th percentile of the following data :
Height (in cm)135140145150155160165170No. of students72032483628244View SolutionThe following table shows the heights of 50 students of a class :
Height (in cm)152148150153149151147Number of students834712106
Find the mean and the median.
Using empirical formula, calculate its mode.View Solution

