The following table given the marks scored by 50 students in a 100 marks test of Mathematics.
Marks0−2020−4040−6060−80No of 31218107students
A student is selected randomly from the class.
Find the probability that the selected student.
The correct Answer is:0.3
To solve the problem, we will follow these steps:
Step 1: Organize the Data
We have the following data from the table:
| Marks | Number of Students |
|-----------|--------------------|
| 0 - 20 | 3 |
| 20 - 40 | 12 |
| 40 - 60 | 18 |
| 60 - 80 | 10 |
| 80 - 100 | 7 |
Step 2: Calculate Total Number of Students
We need to find the total number of students. We will sum the number of students in each category.
Total Students = 3 + 12 + 18 + 10 + 7
Total Students = 50
Step 3: Find Probability of Selected Student Scoring Less than 40 Marks
To find the probability that a randomly selected student scored less than 40 marks, we need to consider the categories that fall below 40 marks, which are:
- 0 - 20: 3 students
- 20 - 40: 12 students
Total students scoring less than 40 = 3 + 12 = 15
Now, we can calculate the probability:
Probability (Less than 40) = (Number of students scoring less than 40) / (Total number of students)
Probability (Less than 40) = 15 / 50
Probability (Less than 40) = 3 / 10
Step 4: Find Probability of Selected Student Scoring 60 or More Marks
Next, we find the probability that a randomly selected student scored 60 marks or more. The relevant categories are:
- 60 - 80: 10 students
- 80 - 100: 7 students
Total students scoring 60 or more = 10 + 7 = 17
Now, we can calculate the probability:
Probability (60 or more) = (Number of students scoring 60 or more) / (Total number of students)
Probability (60 or more) = 17 / 50
Final Answers
1. Probability of a student scoring less than 40 marks = 3/10
2. Probability of a student scoring 60 or more marks = 17/50
---
We have the following data from the table:
|-----------|--------------------|
| 0 - 20 | 3 |
| 20 - 40 | 12 |
| 40 - 60 | 18 |
| 60 - 80 | 10 |
| 80 - 100 | 7 |
We need to find the total number of students. We will sum the number of students in each category.
Total Students = 50
To find the probability that a randomly selected student scored less than 40 marks, we need to consider the categories that fall below 40 marks, which are:
- 20 - 40: 12 students
Probability (Less than 40) = 15 / 50
Probability (Less than 40) = 3 / 10
Next, we find the probability that a randomly selected student scored 60 marks or more. The relevant categories are:
- 80 - 100: 7 students
Probability (60 or more) = 17 / 50
1. Probability of a student scoring less than 40 marks = 3/10
2. Probability of a student scoring 60 or more marks = 17/50
Topper's Solved these Questions
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - EXERCISE 15.1
23 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Multiple Choice Questions (MCQs)
10 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Multiple Choice Questions (MCQs)
10 Videos
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Multiple Choice Questions MCQs)
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
The following table given the marks scored by 50 students in a 100 marks test of Mathematics.
Marks0−2020−4040−6060−80No of 31218107students
A student is selected randomly from the class.
Find the probability that selected student has scored 60 or more than 60 marks.
View SolutionThe following table represent marks obtained by 100 students in a test.
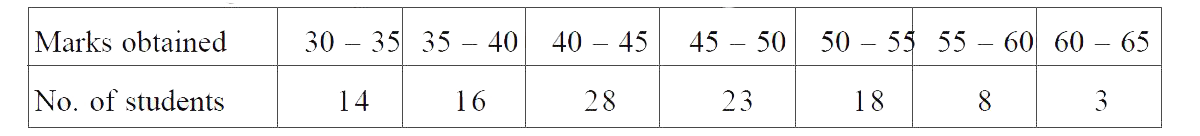
Find mean marks of the students.
View SolutionMarks scored by 100 students in a 25 marks unit test of Mathematics is given below. Their median is
View SolutionThe following information gives the marks scored by the students of a class in an examination. Find the mode of the data. Marks1−2021−4041−6061−8081−100Number of Students318233719
View SolutionThe following table gives the marks scored by 100 students in an entrance examination.

View SolutionThere are 60 boys and 40 girls in a class. A student is selected at random.Find the probability that student is a girl.
View SolutionFollowing table shows the marks scored by a group of 90 students in a mathematics test of 100 marks. Marks 0-20 20-30 30-40 40-50 50-60 60-70 70-100 No. of Students: 7 10 10 20 20 15 8 Find the probability that marks scored by a student in the class is: at most 60 marks (ii) at least 60 marks (iii)not more than 50 marks
View SolutionThe table given below shows the marks obtained by 50 students of a class in a test with maximum marks 100.
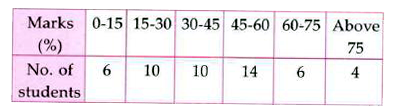
A student of the class is selected at random. Find the probability that the selected student gets
marks equal to or greater than 45% but less than 60%.
View SolutionThe following table shows marks secured by the students of a class in an examination in English:
Marks0−1010−2020−3030−4040−50Number of Students 20 24 40 36 20
Calculte mean marks using Short-cut Method.
View SolutionThe following table shows marks secured by the students of a class in an examination in English:
Marks0−1010−2020−3030−4040−50Number of Students 20 24 40 36 20
Calculte mean marks using Short-cut Method.
View Solution
