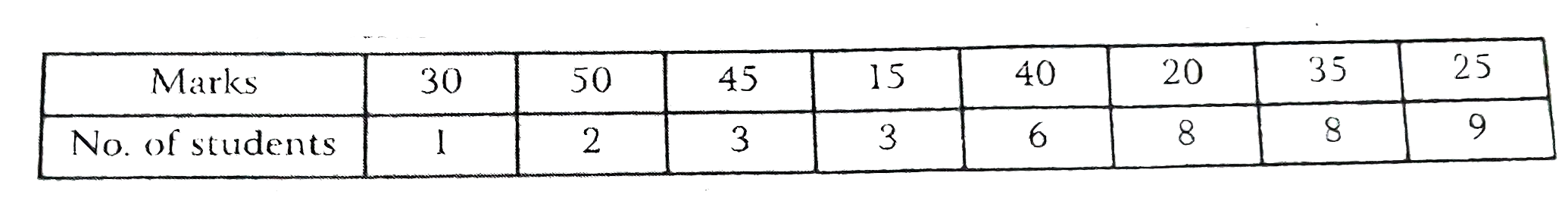Following table shows the marks scored by a group of 90 students in a mathematics test of 100 marks. Marks 0-20 20-30 30-40 40-50 50-60 60-70 70-100 No. of Students: 7 10 10 20 20 15 8 Find the probability that marks scored by a student in the class is: at most 60 marks (ii) at least 60 marks (iii)not more than 50 marks
To solve the problem, we will calculate the probabilities for each of the three scenarios based on the given frequency distribution of marks scored by 90 students.
Given Data:
- Marks Ranges and Number of Students:
- 0-20: 7 students
- 20-30: 10 students
- 30-40: 10 students
- 40-50: 20 students
- 50-60: 20 students
- 60-70: 15 students
- 70-100: 8 students
Total Number of Students:
Total = 7 + 10 + 10 + 20 + 20 + 15 + 8 = 90 students
(i) Probability that marks scored by a student is at most 60 marks:
To find the probability of scoring at most 60 marks, we need to count the number of students who scored 60 marks or less.
- Students scoring at most 60 marks:
- 0-20: 7 students
- 20-30: 10 students
- 30-40: 10 students
- 40-50: 20 students
- 50-60: 20 students
Total students scoring at most 60 marks = 7 + 10 + 10 + 20 + 20 = 67 students
Probability (P) = Number of favorable outcomes / Total outcomes
P(at most 60 marks)=6790
(ii) Probability that marks scored by a student is at least 60 marks:
To find the probability of scoring at least 60 marks, we count the number of students who scored 60 marks or more.
- Students scoring at least 60 marks:
- 60-70: 15 students
- 70-100: 8 students
Total students scoring at least 60 marks = 15 + 8 = 23 students
Probability (P) = Number of favorable outcomes / Total outcomes
P(at least 60 marks)=2390
(iii) Probability that marks scored by a student is not more than 50 marks:
To find the probability of scoring not more than 50 marks, we count the number of students who scored 50 marks or less.
- Students scoring not more than 50 marks:
- 0-20: 7 students
- 20-30: 10 students
- 30-40: 10 students
- 40-50: 20 students
Total students scoring not more than 50 marks = 7 + 10 + 10 + 20 = 47 students
Probability (P) = Number of favorable outcomes / Total outcomes
P(not more than 50 marks)=4790
Summary of Probabilities:
1. Probability of at most 60 marks: 6790
2. Probability of at least 60 marks: 2390
3. Probability of not more than 50 marks: 4790
- Marks Ranges and Number of Students:
- 0-20: 7 students
- 20-30: 10 students
- 30-40: 10 students
- 40-50: 20 students
- 50-60: 20 students
- 60-70: 15 students
- 70-100: 8 students
Total = 7 + 10 + 10 + 20 + 20 + 15 + 8 = 90 students
To find the probability of scoring at most 60 marks, we need to count the number of students who scored 60 marks or less.
- 0-20: 7 students
- 20-30: 10 students
- 30-40: 10 students
- 40-50: 20 students
- 50-60: 20 students
P(at most 60 marks)=6790
To find the probability of scoring at least 60 marks, we count the number of students who scored 60 marks or more.
- 60-70: 15 students
- 70-100: 8 students
P(at least 60 marks)=2390
To find the probability of scoring not more than 50 marks, we count the number of students who scored 50 marks or less.
- 0-20: 7 students
- 20-30: 10 students
- 30-40: 10 students
- 40-50: 20 students
P(not more than 50 marks)=4790
1. Probability of at most 60 marks: 6790
2. Probability of at least 60 marks: 2390
3. Probability of not more than 50 marks: 4790
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a class test, a student scored 8 marks out of 25 marks. The student's marks in percentage is:
A32B35C29D30 - Question 2 - Select One
In a class test, a student scored 8 marks out of 25 marks. The student's marks in percentage is:
AA)32BB)35CC)29DD)30
The following table shows the distribution of the percentage of marks of a group of students:
Percentage of Marks30−4040−5050−6060−7070−8080−90Number of Students4113752View SolutionThe following table given the marks scored by 50 students in a 100 marks test of Mathematics.
Marks0−2020−4040−6060−80No of 31218107students
A student is selected randomly from the class.
Find the probability that the selected student.View SolutionThe following table given the marks scored by 50 students in a 100 marks test of Mathematics.
Marks0−2020−4040−6060−80No of 31218107students
A student is selected randomly from the class.
Find the probability that selected student has scored 60 or more than 60 marks.View SolutionFollowing are the marks obtained by 30 students in a examination

Taking class intervals 0−10,10−20,…..40−50 construct a frequency table.View SolutionFind the about the mean for the following data:
Marks obtained , 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80
Number of students, 2, 3, 8, 14, 8, 3, 2View SolutionThe following table shows the marks of 90 students in a test of 80 marks :
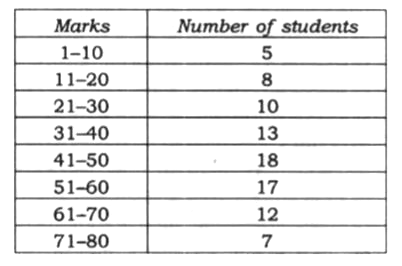
The percentage of students who have obtained less than or equal to 50% marks isView Solution