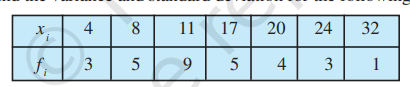
The following table gives the number of finished articles turned out
per day be different number of workers in a factors. Find the standard
deviation of the daily output of finished articles.
Find the variance and standard deviation of the following frequency
distribution:
Number of
article:, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27
No. of
workers:, 3, 7, 11, 14, 18, 17, 13, 8, 5, 4
To find the variance and standard deviation of the given frequency distribution, we will follow these steps:
Step 1: Create a Frequency Table
We will create a table with the number of articles (x) and the corresponding number of workers (f).
| Number of Articles (x) | Number of Workers (f) |
|------------------------|-----------------------|
| 18 | 3 |
| 19 | 7 |
| 20 | 11 |
| 21 | 14 |
| 22 | 18 |
| 23 | 17 |
| 24 | 13 |
| 25 | 8 |
| 26 | 5 |
| 27 | 4 |
Step 2: Calculate the Mean
First, we need to calculate the mean (μ) of the distribution.
Mean(μ)=∑(f⋅x)∑f
Calculating f⋅x:
f⋅x:3⋅18=547⋅19=13311⋅20=22014⋅21=29418⋅22=39617⋅23=39113⋅24=3128⋅25=2005⋅26=1304⋅27=108
Now, summing these products:
∑(f⋅x)=54+133+220+294+396+391+312+200+130+108=2048
Calculating ∑f:
∑f=3+7+11+14+18+17+13+8+5+4=100
Now we can find the mean:
μ=2048100=20.48
Step 3: Calculate the Deviations
Next, we calculate the deviation of each article count from the mean (di = xi - μ):
| Number of Articles (x) | Number of Workers (f) | x−μ (di) |
|------------------------|-----------------------|-----------------|
| 18 | 3 | -2.48 |
| 19 | 7 | -1.48 |
| 20 | 11 | -0.48 |
| 21 | 14 | 0.52 |
| 22 | 18 | 1.52 |
| 23 | 17 | 2.52 |
| 24 | 13 | 3.52 |
| 25 | 8 | 4.52 |
| 26 | 5 | 5.52 |
| 27 | 4 | 6.52 |
Step 4: Calculate f⋅(x−μ)2
Now we will calculate f⋅(di)2:
f⋅(di)2:3⋅(−2.48)2=18.4327⋅(−1.48)2=7.63211⋅(−0.48)2=2.54414⋅(0.52)2=3.80818⋅(1.52)2=41.08817⋅(2.52)2=106.36813⋅(3.52)2=154.3688⋅(4.52)2=163.4885⋅(5.52)2=152.884⋅(6.52)2=170.88
Now summing these products:
∑f⋅(di)2=18.432+7.632+2.544+3.808+41.088+106.368+154.368+163.488+152.88+170.88=670.088
Step 5: Calculate Variance
Now we can calculate the variance (σ²):
σ²=∑f⋅(di)2∑f−(∑f⋅x∑f)2
σ²=670.088100−(20.48)2
Calculating (20.48)2=419.4304:
σ²=6.70088−419.4304=251.70088
Step 6: Calculate Standard Deviation
Finally, the standard deviation (σ) is the square root of the variance:
σ=√251.70088≈15.85
Final Answers
- Variance (σ²) ≈ 251.70
- Standard Deviation (σ) ≈ 15.85
We will create a table with the number of articles (x) and the corresponding number of workers (f).
|------------------------|-----------------------|
| 18 | 3 |
| 19 | 7 |
| 20 | 11 |
| 21 | 14 |
| 22 | 18 |
| 23 | 17 |
| 24 | 13 |
| 25 | 8 |
| 26 | 5 |
| 27 | 4 |
First, we need to calculate the mean (μ) of the distribution.
Next, we calculate the deviation of each article count from the mean (di = xi - μ):
|------------------------|-----------------------|-----------------|
| 18 | 3 | -2.48 |
| 19 | 7 | -1.48 |
| 20 | 11 | -0.48 |
| 21 | 14 | 0.52 |
| 22 | 18 | 1.52 |
| 23 | 17 | 2.52 |
| 24 | 13 | 3.52 |
| 25 | 8 | 4.52 |
| 26 | 5 | 5.52 |
| 27 | 4 | 6.52 |
Now we will calculate f⋅(di)2:
Now we can calculate the variance (σ²):
Finally, the standard deviation (σ) is the square root of the variance:
- Variance (σ²) ≈ 251.70
- Standard Deviation (σ) ≈ 15.85
Topper's Solved these Questions
Similar Questions
Knowledge Check
The standard deviation of the following frequency distribution
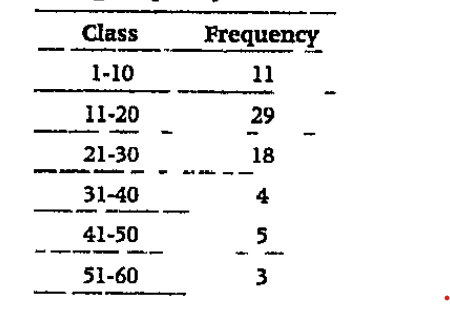 A12.7B13.6C15.3DNone of these
A12.7B13.6C15.3DNone of these
Find the variance and standard deviation from the following data:

View SolutionCalculate variance and standard deviation for the following distribution.

View SolutionCalculate mean, Variance and Standard Deviation for the following distribution.

View SolutionFind out the standard deviation from the following distribution table:

View SolutionFind the variance and standard deviation of the following data : 4,6,10,12,14,18,20
View SolutionFind the mean variance and standard deviation for the following data: 2,4,5,6,8,17
View SolutionFind the mean, variance and standard deviation of first n natural numbers.
View Solution