The following table shows the marks scored by 140 students in an examination of a certain paper: Marks: 0-10 10-20 20-30 30-40 40-50 No. of students: 20 24 40 36 20 Calculate the average marks by using the assumed mean deviation method.
To calculate the average marks using the assumed mean deviation method, we will follow these steps:
Step 1: Create a Frequency Table
We start by organizing the data into a frequency table, including class intervals and the number of students (frequency).
| Marks | No. of Students (f) |
|-----------|----------------------|
| 0 - 10 | 20 |
| 10 - 20 | 24 |
| 20 - 30 | 40 |
| 30 - 40 | 36 |
| 40 - 50 | 20 |
| Total | 140 |
Step 2: Calculate Class Marks (x_i)
The class mark (x_i) for each class interval is calculated as the average of the lower and upper limits of each interval.
- For 0 - 10: x1=0+102=5
- For 10 - 20: x2=10+202=15
- For 20 - 30: x3=20+302=25
- For 30 - 40: x4=30+402=35
- For 40 - 50: x5=40+502=45
| Marks | No. of Students (f) | Class Marks (x_i) |
|-----------|----------------------|--------------------|
| 0 - 10 | 20 | 5 |
| 10 - 20 | 24 | 15 |
| 20 - 30 | 40 | 25 |
| 30 - 40 | 36 | 35 |
| 40 - 50 | 20 | 45 |
Step 3: Assume the Mean (a)
We will assume the mean (a) to be the class mark of the modal class. Here, the modal class is 20 - 30, so we take:
a=25
Step 4: Calculate Deviations (d_i)
Calculate the deviations (d_i) from the assumed mean (a).
- d1=x1−a=5−25=−20
- d2=x2−a=15−25=−10
- d3=x3−a=25−25=0
- d4=x4−a=35−25=10
- d5=x5−a=45−25=20
Step 5: Calculate f_i * d_i
Now, we calculate the product of frequency (f_i) and deviations (d_i).
| Marks | No. of Students (f) | Class Marks (x_i) | Deviations (d_i) | f_i * d_i |
|-----------|----------------------|--------------------|-------------------|------------|
| 0 - 10 | 20 | 5 | -20 | -400 |
| 10 - 20 | 24 | 15 | -10 | -240 |
| 20 - 30 | 40 | 25 | 0 | 0 |
| 30 - 40 | 36 | 35 | 10 | 360 |
| 40 - 50 | 20 | 45 | 20 | 400 |
| Total | 140 | | | 120 |
Step 6: Calculate the Average Marks (x̄)
Using the formula for the average marks:
¯x=a+Σ(fidi)Σfi
Substituting the values:
¯x=25+120140
¯x=25+0.8571≈25.8571
Thus, the average marks of the students is approximately 25.86.
We start by organizing the data into a frequency table, including class intervals and the number of students (frequency).
|-----------|----------------------|
| 0 - 10 | 20 |
| 10 - 20 | 24 |
| 20 - 30 | 40 |
| 30 - 40 | 36 |
| 40 - 50 | 20 |
| Total | 140 |
The class mark (x_i) for each class interval is calculated as the average of the lower and upper limits of each interval.
- For 10 - 20: x2=10+202=15
- For 20 - 30: x3=20+302=25
- For 30 - 40: x4=30+402=35
- For 40 - 50: x5=40+502=45
|-----------|----------------------|--------------------|
| 0 - 10 | 20 | 5 |
| 10 - 20 | 24 | 15 |
| 20 - 30 | 40 | 25 |
| 30 - 40 | 36 | 35 |
| 40 - 50 | 20 | 45 |
We will assume the mean (a) to be the class mark of the modal class. Here, the modal class is 20 - 30, so we take:
Calculate the deviations (d_i) from the assumed mean (a).
- d2=x2−a=15−25=−10
- d3=x3−a=25−25=0
- d4=x4−a=35−25=10
- d5=x5−a=45−25=20
Now, we calculate the product of frequency (f_i) and deviations (d_i).
|-----------|----------------------|--------------------|-------------------|------------|
| 0 - 10 | 20 | 5 | -20 | -400 |
| 10 - 20 | 24 | 15 | -10 | -240 |
| 20 - 30 | 40 | 25 | 0 | 0 |
| 30 - 40 | 36 | 35 | 10 | 360 |
| 40 - 50 | 20 | 45 | 20 | 400 |
| Total | 140 | | | 120 |
Using the formula for the average marks:
¯x=25+0.8571≈25.8571
Topper's Solved these Questions
Similar Questions
Following are the marks obtained by 30 students in a examination

Taking class intervals 0−10,10−20,…..40−50 construct a frequency table.View SolutionThe following table gives the marks scored by 100 students in an entrance examination. Marks: 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 No. of Students (Frequency): 4 10 16 22 20 18 8 2 Represent this data in the form of a histogram.
View SolutionFind the deviation from the mean and from median of the following distribution: Marks 0-10 10-20 20-30 30-40 40-50 No. of Students 5 8 15 16 6
View SolutionThe following table gives the marks scored by 378 students in an entrance examination : Marks 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100 No. of Students 3 12 36 76 97 85 39 12 12 6 From this table form (i) less than series, and (ii) the more than series.
View SolutionMarks of 40 student in a test out of maximum 50 marks are as follow :
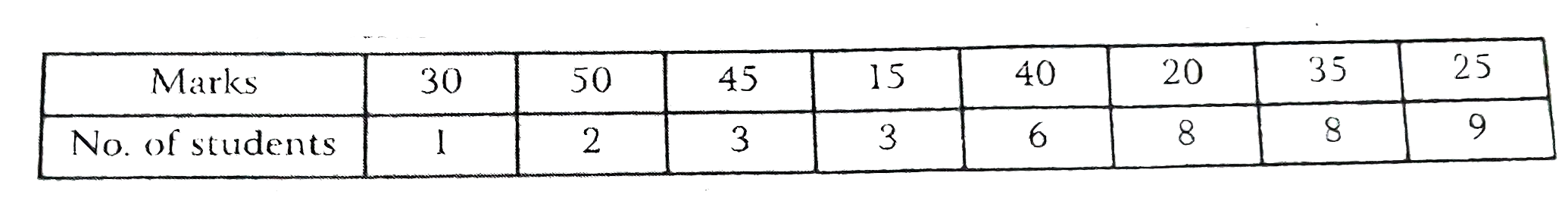 View Solution
View SolutionFind the mode of the following frequency table, which gives the marks scored by 40 students in a test:
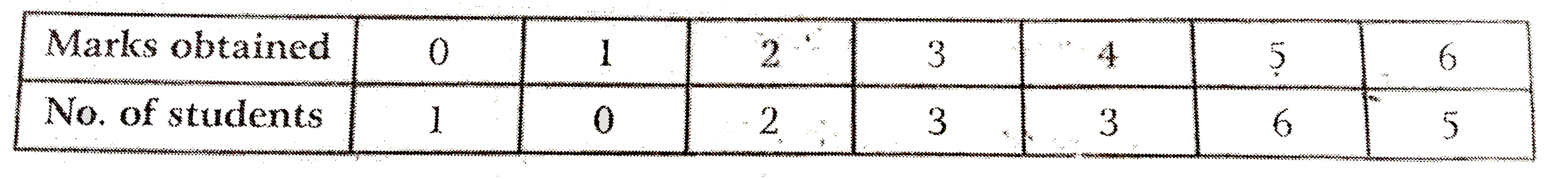 View Solution
View SolutionFind the mode of the following distribution of marks obtained by 80 students: Marks obtained 0-10 10-20 20-30 30-40 40-50 No. of students 6 10 12 32 20
View SolutionFind the mode of the following distribution of marks obtained by 80 students: Marks obtained 0-10 10-20 20-30 30-40 40-50 No. of students 6 10 12 32 20
View SolutionFind the mode of the following distribution of marks obtained by 80 students: Marks obtained 0-10 10-20 20-30 30-40 40-50 No. of students 6 10 12 32 20
View SolutionFollowing table shows the marks scored by a group of 90 students in a mathematics test of 100 marks. Marks 0-20 20-30 30-40 40-50 50-60 60-70 70-100 No. of Students: 7 10 10 20 20 15 8 Find the probability that marks scored by a student in the class is: at most 60 marks (ii) at least 60 marks (iii)not more than 50 marks
View Solution

