Marks of 40 student in a test out of maximum 50 marks are as follow :
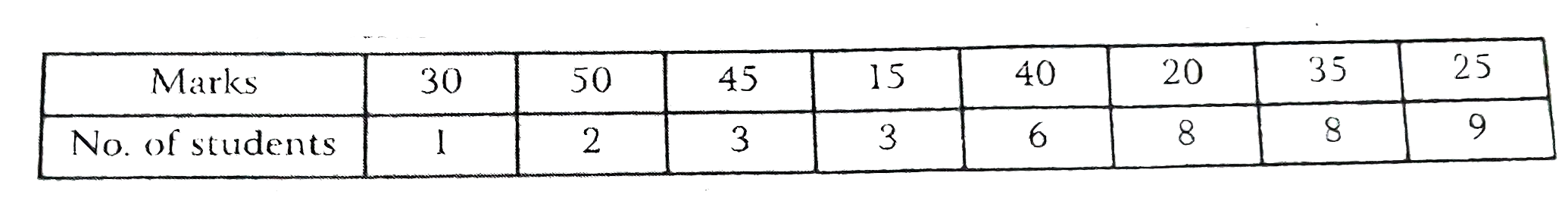
To find the median, it is necessary to arrange the dat in ascending or desecending order of their magnitude. So, on arranging the data in ascending order, we get the following table :

Here N-40, which is even
∴Median=N2thvalue+(N2+1)thevalue40thvalue+(402+1)thvalue
=20thvalue+21stvalue2=25+302=27.5
Topper's Solved these Questions
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Problems From NCERT/exemplar
4 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Exercise 14 A
17 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Long Answer Questions
5 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
1 Videos
Similar Questions
In a class of 40 students, the marks obtained (out of 50) are as given below:
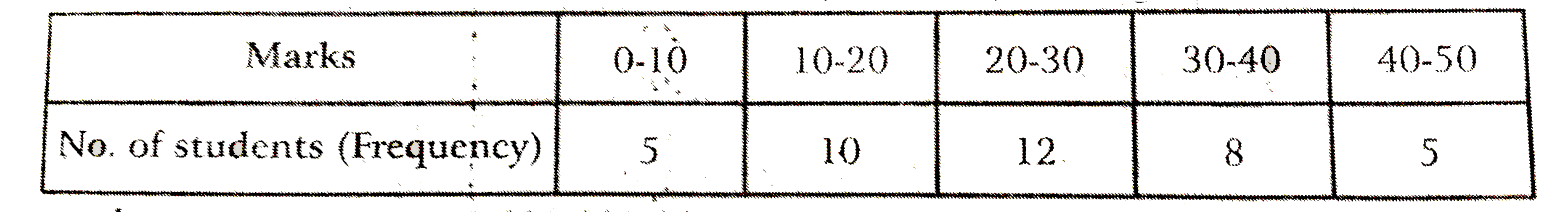
Draw a histogram to represent the given data.
View SolutionThe marks of 12 students in a Math test are as follows: 8,10,4,8,5,6,9,7,6,8,9,10 Find the: a maximum marks, b. minimum marks, c. range of marks, and d. mean marks.
View Solution
Knowledge Check
Marks of 10 students in an English test are as follow, 9,10,7,11,12,6,8,14,15,18. Find.
Maximum marks obtainedA20B43C18D8Marks of 10 students in an English test are as follow, 9,10,7,11,12,6,8,14,15,18. Find.
Range of the marksA11B12C15D18Marks of 10 students in an English test are as follow, 9,10,7,11,12,6,8,14,15,18. Find mean marks
A15B12C11D18
The marks of some students were listed out of a maximum 75. The SD of marks was found to be 9. Subsequently the marks were raised to a maximum of 100 and variance of new marks was calculated. The new variance is (1)144 (2) 122 (3) 81 (4) None of these
View SolutionThe marks of some students were listed out of a maximum 75. The SD of marks was found to be 9. Subsequently the marks were raised to a maximum of 100 and variance of new marks was calculated. The new variance is 144 2. 122 3. 81 4. 256 5. 16
View SolutionThe frequency distribution of the marks obtained by 100 students in a test carrying 50 marks is given below. Then the mean is
Marks 0−910−1920−2930−3940−49No. of students 8 15 20 45 12
View SolutionFollowing table shows the marks scored by a group of 90 students in a mathematics test of 100 marks. Marks 0-20 20-30 30-40 40-50 50-60 60-70 70-100 No. of Students: 7 10 10 20 20 15 8 Find the probability that marks scored by a student in the class is: at most 60 marks (ii) at least 60 marks (iii)not more than 50 marks
View SolutionThe frequency distribution of marks obtained by 28 students in a test carrying 40 marks is given below:
Marks:0−1010−2020−3030−40Number of students:6xy6
If the mean of the above data is 20, then the difference between x and y is
View Solution
