The formula above is Newton's law of universal gratitation, where F is the attractive force, γ is the gravitational constnat, m1andm2 are the masses of the particles, and r is the distnace between their centres of mass. Which of the following givers r in terms of F,γ,m1,andm2?
r=√(m1)(m2)γ(m2)
r=√F(m2)γ(m1)
r=√γ(m2)F(m1)
r=√γ(m1)(m2)F
The correct Answer is:D
To solve for r in terms of F,γ,m1, and m2 using Newton's law of universal gravitation, we start with the formula:
F=γ⋅m1⋅m2r2
Step 1: Rearranging the equation
We want to isolate r2 on one side of the equation. To do this, we can multiply both sides by r2 and then divide both sides by F:
F⋅r2=γ⋅m1⋅m2
Step 2: Isolating r2
Next, we divide both sides by F to isolate r2:
r2=γ⋅m1⋅m2F
Step 3: Taking the square root
To find r, we take the square root of both sides:
r=√γ⋅m1⋅m2F
Conclusion
Thus, the expression for r in terms of F,γ,m1, and m2 is:
r=√γ⋅m1⋅m2F
Final Answer
The correct option is option 4:
r=√γ⋅m1⋅m2F
---
We want to isolate r2 on one side of the equation. To do this, we can multiply both sides by r2 and then divide both sides by F:
Next, we divide both sides by F to isolate r2:
To find r, we take the square root of both sides:
Thus, the expression for r in terms of F,γ,m1, and m2 is:
The correct option is option 4:
Topper's Solved these Questions
- LINEAR EQUATIONS AND GRAPHSBOOK - KAPLANCHAPTER - LINEAR EQUATIONS AND GRAPHSEXERCISE - TRY YOUR OWN
26 Videos
- LINEAR EQUATIONS AND GRAPHSBOOK - KAPLANCHAPTER - LINEAR EQUATIONS AND GRAPHSEXERCISE - SOLVING EQUATIONS
1 Videos
- INEQUALITIESBOOK - KAPLANCHAPTER - INEQUALITIESEXERCISE - MODELING REAL-LIFE SITUATIONS WITH INEQUALITIES
1 Videos
- PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES BOOK - KAPLANCHAPTER - PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES EXERCISE - HOW MUCH HAVE YOU LEARNED
11 Videos
Similar Questions
Knowledge Check
Two stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
A2π√r32G(m1+m2)B2π√r3(m1+m2)2G(m1m2)C2π√2r3G(m1+m2)D2π√r3G(m1+m2)The gravitational force between a H-atom and another particle of mass m will be given by Newton's law
F=GM.mr2, where r is in km andAM=mproton+melectronBM=mproton+melectron−Bc2 (B=13.6 eV)CM is not related to the mass of hydrogen atomDM=mproton+melectron−|V|c2(|V|=magnitude of the potential energy of electron in the H-atom )
If two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionF=Gm1,m2/d2 is the equation representing Newton's law of universal gravitation. Which of the statements below is true?
View SolutionLet r be the distance of a particle from a fixed point to which it is attracted by an inverse square law force given by F=k/r2 (k=constant). Let m be the mass of the particle and L be its angular momentum with respect to the fixed point. Which of the following formulae is correct about the total energy of the system?
View SolutionIn the arragement of figure assume negligible friction between the blocks and table. If F the pulling force and m1 and m2 the masses are known, then the tension in the string is :
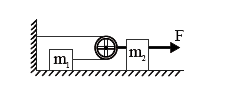
View SolutionThe gravitational force between a H-atom and another particle of mass m will be given by Newton's law: F=GM.mr2, where r is in km and
View SolutionThe gravitational force between a H-atom and another particle of mass m will be given by Newton's law: F=GM.mr2, where r is in km and
View Solution
