The gravitational force between a H-atom and another particle of mass m will be given by Newton's law: F=GM.mr2, where r is in km and
M=Mproton+melectron
M=Mproton+melectron−BC2(B=13.6eV)
M is not relate to the mass of the hydrogen atom
M=Mproton+melectron−|V|c2|V|= magnitude of the potential energy of electron in the H-atom
The correct Answer is:B
To solve the problem of calculating the gravitational force between a hydrogen atom and another particle of mass m, we will follow these steps:
Step 1: Identify the mass of the hydrogen atom
The mass of a hydrogen atom is primarily determined by its nucleus, which consists of one proton, and it also includes the mass of one electron. Therefore, the effective mass M of the hydrogen atom can be expressed as:
M=mp+me
Where:
- mp is the mass of the proton (approximately 1.67×10−27 kg)
- me is the mass of the electron (approximately 9.11×10−31 kg)
Step 2: Calculate the total mass of the hydrogen atom
Now, we can calculate the total mass of the hydrogen atom:
M=1.67×10−27 kg+9.11×10−31 kg≈1.67×10−27 kg(since mp≫me)
Step 3: Consider the binding energy
When a hydrogen atom is formed, some mass is converted into energy, known as binding energy. According to Einstein's mass-energy equivalence principle, this can be expressed as:
E=mc2
The binding energy B of a hydrogen atom is approximately 13.6 eV. To convert this energy into mass, we use:
m=Bc2
Where c is the speed of light (c≈3×108 m/s). First, we need to convert the binding energy from eV to joules:
B=13.6 eV×1.6×10−19 J/eV≈2.18×10−18 J
Now we can calculate the equivalent mass:
m=2.18×10−18 J(3×108 m/s)2≈2.18×10−189×1016≈2.43×10−35 kg
Step 4: Adjust the mass of the hydrogen atom
Now we can adjust the mass of the hydrogen atom to account for the binding energy:
Mactual=M−m
Substituting the values we have:
Mactual=(1.67×10−27 kg)−(2.43×10−35 kg)≈1.67×10−27 kg(since m is negligible)
Step 5: Calculate the gravitational force
Now we can calculate the gravitational force F between the hydrogen atom and another particle of mass m using Newton's law of gravitation:
F=GMmr2
Where G is the gravitational constant (G≈6.674×10−11 N m2/kg2) and r is the distance between the two masses in meters (remember to convert kilometers to meters).
Final Calculation
Assuming r is given in kilometers, convert it to meters:
r (in meters)=r (in kilometers)×1000
Substituting the values into the gravitational force equation will give you the final answer.
The mass of a hydrogen atom is primarily determined by its nucleus, which consists of one proton, and it also includes the mass of one electron. Therefore, the effective mass M of the hydrogen atom can be expressed as:
- mp is the mass of the proton (approximately 1.67×10−27 kg)
- me is the mass of the electron (approximately 9.11×10−31 kg)
Now, we can calculate the total mass of the hydrogen atom:
When a hydrogen atom is formed, some mass is converted into energy, known as binding energy. According to Einstein's mass-energy equivalence principle, this can be expressed as:
Now we can adjust the mass of the hydrogen atom to account for the binding energy:
Now we can calculate the gravitational force F between the hydrogen atom and another particle of mass m using Newton's law of gravitation:
Assuming r is given in kilometers, convert it to meters:
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - NUCLEIEXERCISE - Very short Anwer type question14videos
NUCLEI
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - NUCLEIEXERCISE - Long answer type question10videos
NUCLEI
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions7videos
MOVING CHARNGES AND MAGNETISM
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS16videos
RAY OPTICS AND OPTICAL INSTRUMENTS
Similar Questions
Assertion : Mass of the rod AB is m1 and of particle P is m2. Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
F=Gm1m2r2
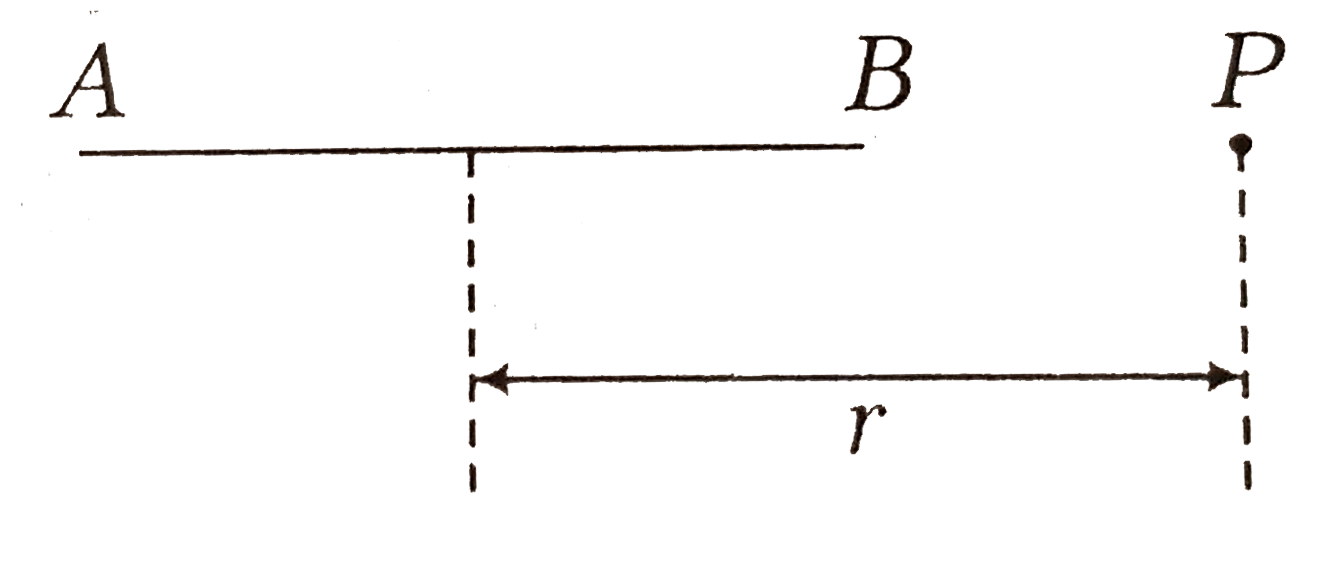
Reason : The relation F=Gm1m2r2 can be applied directly only to find force between two particles.View SolutionA spherical shell has inner radius R1, outer radius R2, and mass M, distributed uniformly throughout the shell. The magnitude of the gravitational force exerted on the shell by a point mass particle of mass m, located at a distance d from the center, inside the inner radius, is:
View Solution
Knowledge Check
- Question 1 - Select One
The gravitational force F between two masses m1andm2 separeted by a distance r is given by
F=Gm1m2r2
Where G is the universal gravitational constant. What are the dimensions of G ?AM−1L2T−3BM−1L3T−2CML3T−2DML2T−3 - Question 2 - Select One
Two sphere of masses m and M are situated in air and the gravitational force between them is F. The space around the masses in now filled with a liquid of specific gravity 3. The gravitational force will now be
A3FBFCF3DF9
Assertion : The centres of two cubes of masses m1andm2 are separated by a distance r. The gravitational force between these two cubes will be Gm1m2r2
Reason : According to Newton's law of gravitation, gravitational force between two point masses m1andm2 separated by a distance r is Gm1m2r2.View SolutionIf gravitational attraction between two points masses be given by F=Gm1m2rn. Then the period of a satellite in a circular orbit will be proportional to
View SolutionTwo sphere of masses m and M are situated in air and the gravitational force between them is F. The space around the masses in now filled with a liquid of specific gravity 3. The gravitational force will now be
View SolutionTwo sphere of masses m and M are situated in air and the gravitational force between them is F. The space around the masses in now filled with a liquid of specific gravity 3. The gravitational force will now be
View SolutionThe gravitational force between two objects is proportional to 1/R (and not as 1/R2) where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
View SolutionThe gravitational force between two objects is proportional to 1/R (and not as 1/R2) where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
View Solution

