The graph of y4−3x2+7=0 is symmetric with respect to which of the following?
the x-axis
the y-axis
the origin
only I
only II
only III
I, II, and III
The correct Answer is:D
To determine the symmetry of the graph of the equation y4−3x2+7=0 with respect to the x-axis, y-axis, and the origin, we will follow these steps:
Step 1: Check for symmetry with respect to the x-axis
To check for symmetry with respect to the x-axis, we replace y with −y in the equation.
Starting with the original equation:
y4−3x2+7=0
Substituting −y for y:
(−y)4−3x2+7=0
Since (−y)4=y4, we have:
y4−3x2+7=0
This is the same as the original equation, indicating that the graph is symmetric with respect to the x-axis.
Step 2: Check for symmetry with respect to the y-axis
To check for symmetry with respect to the y-axis, we replace x with −x in the equation.
Starting with the original equation:
y4−3x2+7=0
Substituting −x for x:
y4−3(−x)2+7=0
Since (−x)2=x2, we have:
y4−3x2+7=0
This is also the same as the original equation, indicating that the graph is symmetric with respect to the y-axis.
Step 3: Check for symmetry with respect to the origin
To check for symmetry with respect to the origin, we replace x with −x and y with −y in the equation.
Starting with the original equation:
y4−3x2+7=0
Substituting −x for x and −y for y:
(−y)4−3(−x)2+7=0
Since (−y)4=y4 and (−x)2=x2, we have:
y4−3x2+7=0
This is the same as the original equation, indicating that the graph is symmetric with respect to the origin.
Conclusion
The graph of the equation y4−3x2+7=0 is symmetric with respect to the x-axis, y-axis, and the origin.
Final Answer
The graph is symmetric with respect to:
- x-axis
- y-axis
- origin
To check for symmetry with respect to the x-axis, we replace y with −y in the equation.
y4−3x2+7=0
(−y)4−3x2+7=0
y4−3x2+7=0
To check for symmetry with respect to the y-axis, we replace x with −x in the equation.
y4−3x2+7=0
y4−3(−x)2+7=0
y4−3x2+7=0
To check for symmetry with respect to the origin, we replace x with −x and y with −y in the equation.
y4−3x2+7=0
(−y)4−3(−x)2+7=0
y4−3x2+7=0
The graph of the equation y4−3x2+7=0 is symmetric with respect to the x-axis, y-axis, and the origin.
The graph is symmetric with respect to:
- x-axis
- y-axis
- origin
Topper's Solved these Questions
Similar Questions
If f(x) is a real-valued function defined as f(x)=In(1−sinx), then the graph of f(x) is (A) symmetric about the line x=π (B) symmetric about the y-axis (C) symmetric and the line x=π2 (D) symmetric about the origin
View SolutionDraw the graph of line 4x+3y=24 Write the coordinates of points where this line intersects the x-axis and y-axis. Use this graph to find the area of the triangle formed by the line and the coordinates axes.
View Solution
Knowledge Check
The graph shows a parabola that is symmetric about the x-axis. Which one of the following could be the equation of the graph?
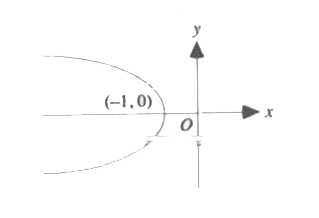 Ax=−y2−1Bx=−y2Cx=−y2+1Dx=y2−1
Ax=−y2−1Bx=−y2Cx=−y2+1Dx=y2−1The equation of parabola through (-1,3) and symmetric with respect to x-axis and vertex at origin is (i) y2=−9x (ii) y2=9x (iii) y2=3x (iv) y2=−3x
Ay2=−9xBy2=9xCy2=3xDy2=−3x
Statement I The graph of y=sec2x is symmetrical about the Y-axis.
Statement II The graph of y=tax is symmetrical about the origin.
View SolutionThe graph of the linear equation 2x−y=4 cuts x-axis at
View SolutionIn a region magnetic field along x axis changes with time according to the given graph.
If time period, pitch and radius of helix path are T0,P0 and R respectively then which of the following is incorrect if the paticle is projected at an angle θ0 with the positive x-axis in x−y plane from origin:
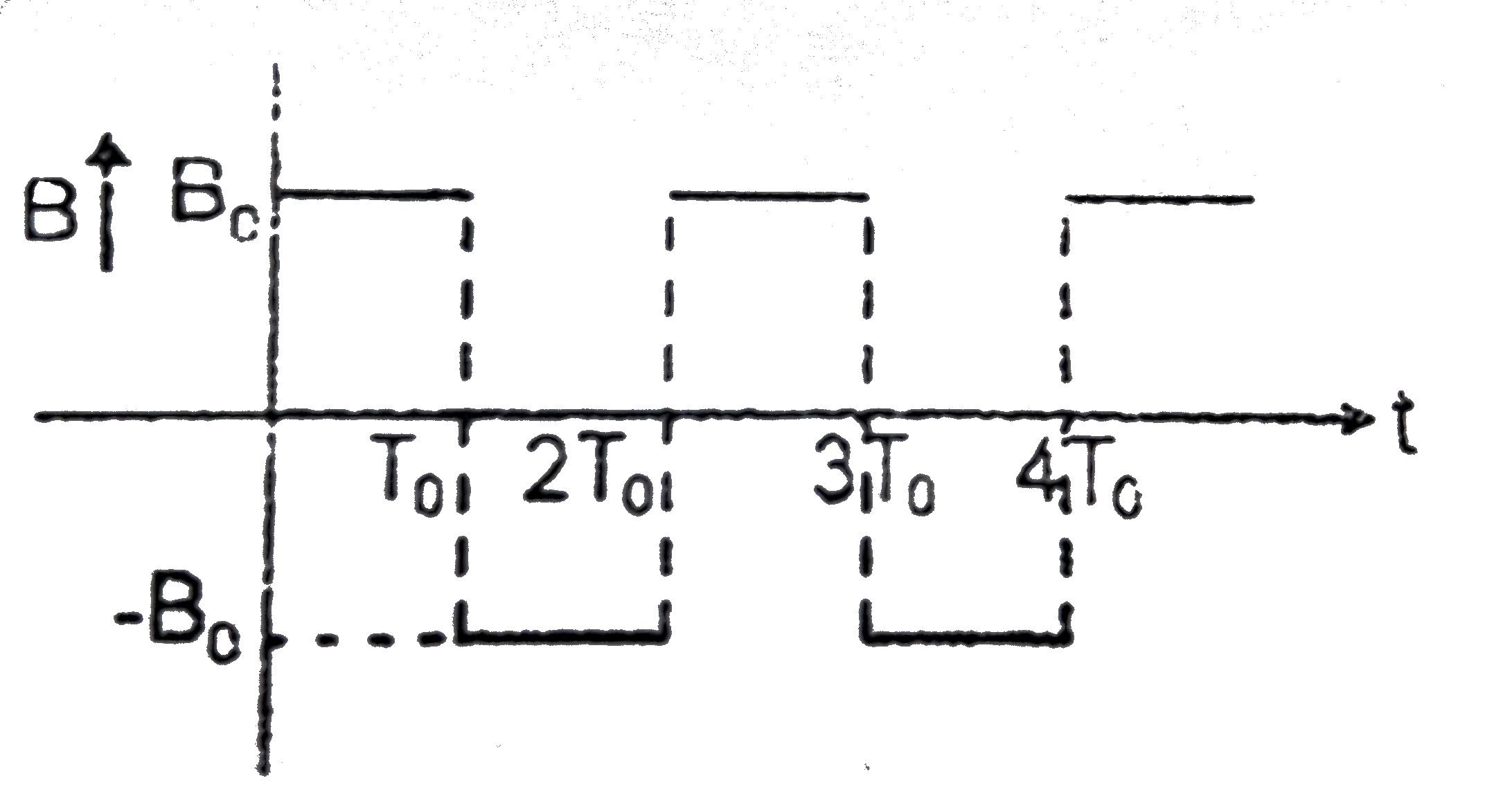
View Solution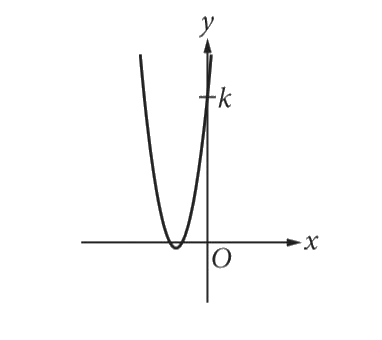
The graph of y=2x2+10x+12 is shown. If the graph crosses the y -axis at the point ( 0, k) , what is the value of k ?
View SolutionSketch the graph of y=√x+1in[0,4] and determine the area of the region enclosed by the curve, the axis of X and the lines x=0,x=4.
View SolutionSuppose R is relation whose graph is symmetric to both X-axis and Y-axis and that the point (1,2) is on the graph of R. Which one of the following is not necessarily on the graph of R?
View Solution
