Question

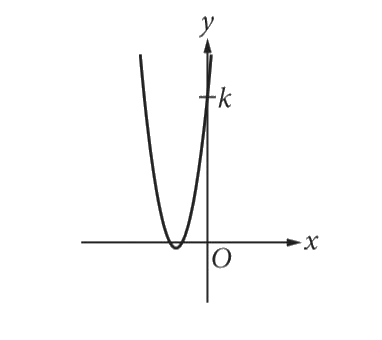
The graph of $y=2x^2+10x+12$ is shown. If the graph crosses the y -axis at the point ( 0, k) , what is the value of k ?

Options

A. 2
B. 6
C. 10
D. 12

Answer

D

Explanation

Since the graph represents the equation `y = 2x^2 + 10x + 12`, it follows that each point (x, y ) on the graph is a solution to this equation. Since the graph crosses the y-axis at (0, k ), then substituting 0 for x and k for y in `y = 2x + 10x + 12^2` creates a true statement: `k = 2(0)^2 + 10(0) + 12`, or k = 12.
Choice A is incorrect. If k = 2 when x = 0, it follows that `2 = 2(0)^2 + 10(0) + 12`, or 2 = 12, which is false. Choice B is incorrect. If k = 6 when x = 0, it follows that `6 = 2(0)^2 + 10(0) + 12`, or 6 = 12, which is false. Choice C is incorrect. If k = 10 when x = 0, it follows that `10 = 2(0)^2 + 10(0) + 12`, or 10 = 12, which is false.