The length of tangent from an external point P on a circle with centre 0 is always less than OP.
To determine whether the statement "The length of tangent from an external point P on a circle with center O is always less than OP" is true or false, we can follow these steps:
Step 1: Understand the Setup
We have a circle with center O and an external point P. A tangent line is drawn from point P to touch the circle at point T.
Hint: Visualize the scenario by sketching a circle with its center and the external point.
Step 2: Identify the Tangent and Radius
The line segment PT represents the length of the tangent from point P to the circle at point T. The line segment OT represents the radius of the circle from the center O to the point of tangency T.
Hint: Remember that a tangent to a circle is always perpendicular to the radius at the point of tangency.
Step 3: Form a Right Triangle
Since the tangent PT is perpendicular to the radius OT at point T, we can form a right triangle OTP. Here, OT is one leg, PT is the other leg, and OP is the hypotenuse.
Hint: Use the properties of right triangles to analyze the relationship between the sides.
Step 4: Apply the Pythagorean Theorem
In triangle OTP, according to the Pythagorean theorem:
OP2=OT2+PT2
This implies that:
OP>PT
because OP is the hypotenuse and must be greater than either of the other two sides.
Hint: Recall that in any right triangle, the hypotenuse is always longer than either leg.
Step 5: Conclude the Statement
Since we have established that OP (the distance from point P to the center O) is greater than PT (the length of the tangent), we can conclude that the statement is true:
PT<OP
Hint: Reiterate that the relationship holds true for any external point and any circle.
Final Conclusion
Thus, the statement "The length of tangent from an external point P on a circle with center O is always less than OP" is indeed true.
We have a circle with center O and an external point P. A tangent line is drawn from point P to touch the circle at point T.
The line segment PT represents the length of the tangent from point P to the circle at point T. The line segment OT represents the radius of the circle from the center O to the point of tangency T.
Since the tangent PT is perpendicular to the radius OT at point T, we can form a right triangle OTP. Here, OT is one leg, PT is the other leg, and OP is the hypotenuse.
In triangle OTP, according to the Pythagorean theorem:
OP2=OT2+PT2
This implies that:
OP>PT
because OP is the hypotenuse and must be greater than either of the other two sides.
Since we have established that OP (the distance from point P to the center O) is greater than PT (the length of the tangent), we can conclude that the statement is true:
PT<OP
Thus, the statement "The length of tangent from an external point P on a circle with center O is always less than OP" is indeed true.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS14videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS14videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
Prove that The length of tangent from an external point on a circle is always greater than the radius of the circle.
View SolutionIn Figure, PA and PB are tangents from an external point P to a circle with centre O . LN touches the circle at M . Prove that PL+LM=PN+MN .
View SolutionIn Fig. 10.76, CP and CQ are tangents from an external point C to a circle with centre O . AB is another tangent which touches the circle at R . If CP=11cm and BR=4cm , find the length of BC . (FIGURE)
View SolutionPA and PB are two tangents drawn from an external point P to a circle with centre C and radius=4cm If PA⊥PB then length of each tangent is
View SolutionIn figure, DE and DF are tangents from an external point D to a circle with centre A. If DE = 5 cm and DE⊥DF, then find the radius of the circle.
 View Solution
View SolutionIn the given figure, TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘. Find angelOPQ.
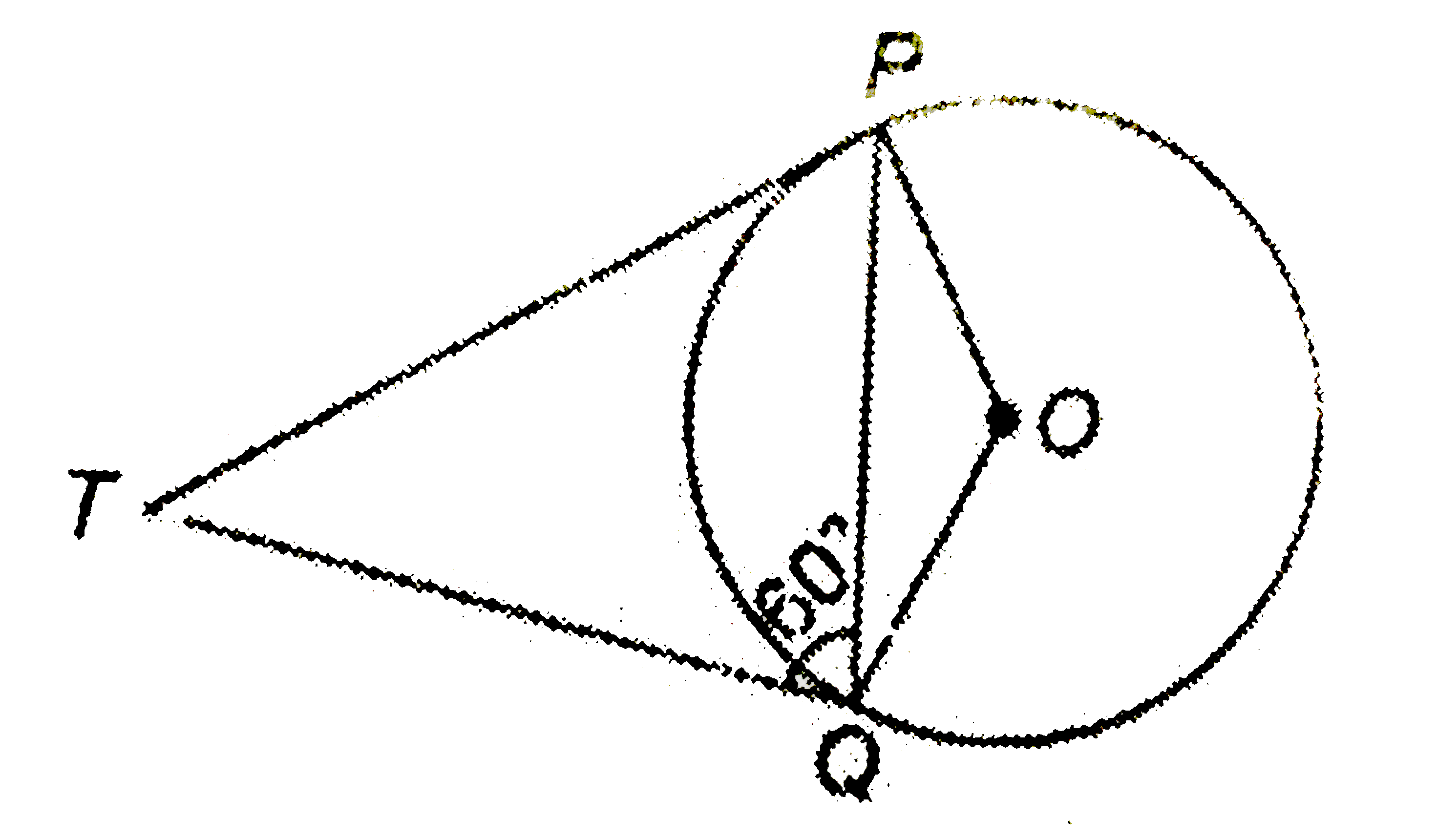 View Solution
View SolutionTwo tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is cyclic quadrilateral.
View SolutionTwo tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View Solution

