The lengths of the sides of a triangle are 23, 32 , and 37 . To the nearest degree , what is the value of the largest angle ?
A
71∘
B
83∘
C
122∘
D
128∘
Video Solution
Text Solution
The correct Answer is:B
The angle opposite the 37 side (call it ∠A) is the largest angle . By the Law of Cosines , 372=232+322−2(23)(32)cosA.
cosA=372−232−322−2(23)(32)≈−184−1,472=0.125 .
Therefore , A=cos−1(0.125)≈83∘.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The lengths of the triangle shown below are rounded to the nearest 0.1 cm. What is the area, to the nearest 1cm2 of the triangle?
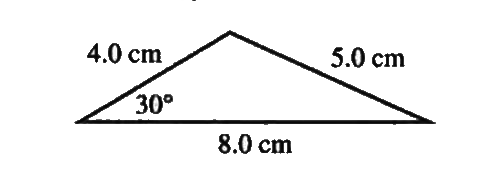
Note: The area of any triangle with sides of length a, b and c opposite angle of measure A, B, and C, respectively, is given by 12absinC.A4B5C8D10The sides of a triangle are in the ratio 4:3:2 . If the perimeter of the triangle is 792, what is the length of the smallest side ?
A176B200C264D352
The sides of triangle are in A.P. and the greatest angle exceeds the least by 90∘. The sides are in the ratio:
View SolutionIf the length of two sides of an isosceles triangle are 3 and 7, what is the perimeter of the triangle?
View SolutionThe lengths of the sides of a triangle are in the ratio 2:3:4. If the perimeter of the triangle is 63 cm, find the lengths of the sides of the triangle.
View SolutionIf the lengths of the sides of a triangle are a - b , a + b and √3a2+b2,(a,b>,0), then the largest angle of the triangle , is
View SolutionIf the length of sides of right angled triangle are in AP, then their ratio is
View SolutionIF the lengths of the side of triangle are 3,5and7, then the largest angle of the triangle is π2 (b) 5π6 (c) 2π3 (d) 3π4
View Solution
