The line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
Line L

A

does not intersect AB

B

does not intersect OB

C

does not intersect OA

D

can intersect all the sides

Text Solution
Verified by Experts

The correct Answer is:C

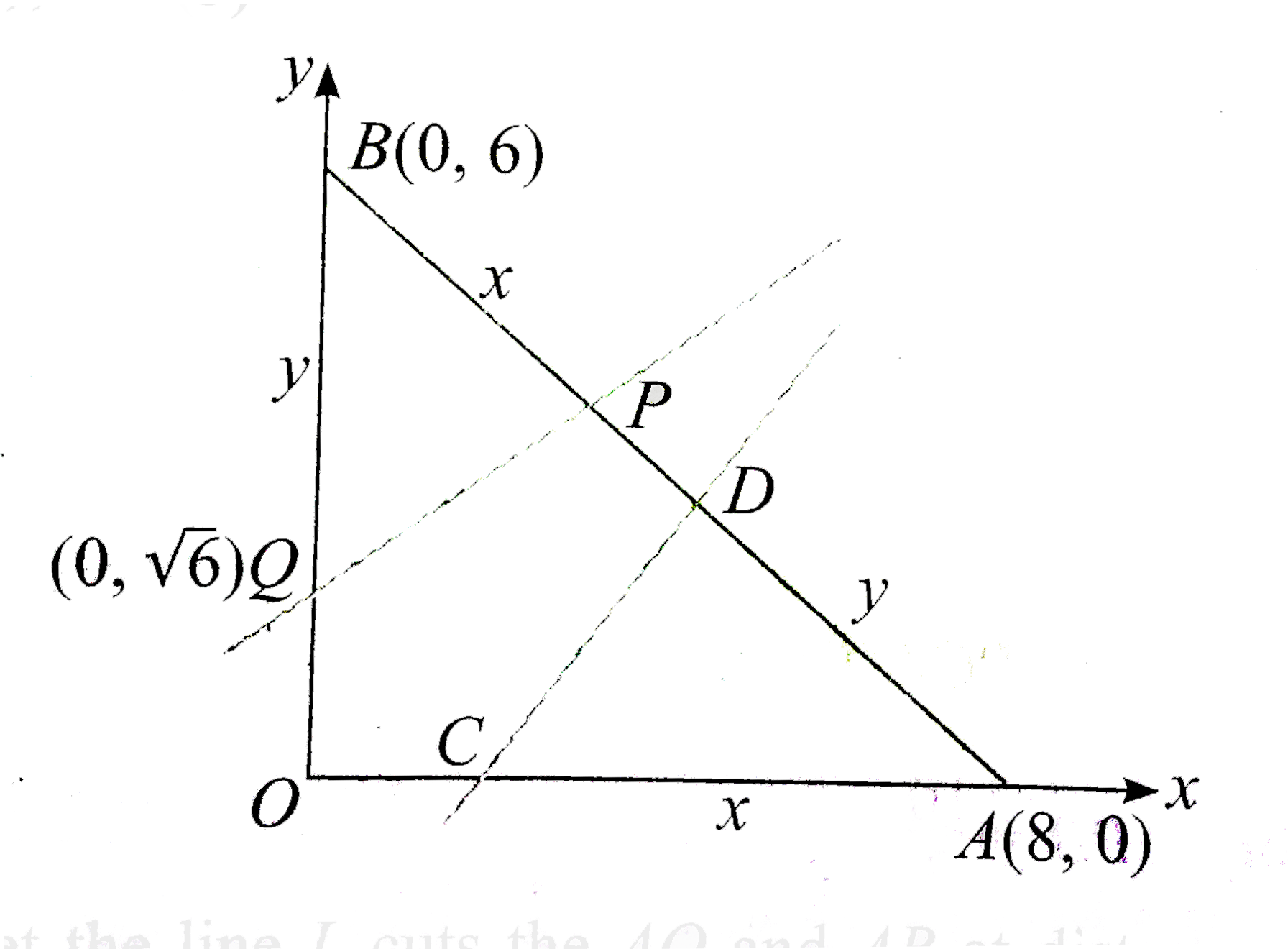
ocr_image
Case I : Let the line L cuts the AO and AB at distances x and y, respectively, from A. Then, the area of the triangle with sides x and y is
12xy sin(∠CAD)=12⋅xy⋅35=3xy10=12
or xy=40
Also, x+y=12 (from perimeter bisection). Then x and y are the roots of r2−12x+40=0 which has imaginary roots.
Case II: if the line L cuts OB and BA at distances y and x, respectively, from B, then we have xy=30 and x+y=12.
Solving, we get x=6+√6 and y=6−√6.
Case III: If the line L cuts the sides OA and OB at distances x and y, respectively, from O, then
x+y=12 and xy=24
∴x,y=6±2√3 (not possible)
So there is a unique line possible. Let point P be (α,β).
Using the parametric equation of AB, we have
β=6−35(6+√6)
and α=45(6+√6)
Hence, the slope of PQ is
β−√6α−0=10−5√610

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
    The slope of line L can be

    A(10+5√6)/10
    B(10−5√6)/10
    C(8+3√6)/10
    Dnone of these

  • The line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
    The number of such lines possible is

    A1
    B2
    C3
    Dmore than 3

  • The line 6x + 8y - 48 intersects the co - ordinate axis at A and B respectively. A line L bisects the area and the perimeter of the traingle OAB, where O is the origin .
    The slope of the line L can be

    A(1−5√6)10
    B(10−5√6)10
    C(8+3√6)10
    Dnone of these