The line joining P(-4, 5) and Q(3, 2) intersects the y-axis at point R. PM and QN are perpendiculars from P and Q on the x-axis. Find:
the ratio PR : RQ
To find the ratio PR : RQ, we will follow these steps:
Step 1: Find the equation of the line joining points P and Q.
The coordinates of points P and Q are P(-4, 5) and Q(3, 2).
The slope (m) of the line joining these two points can be calculated using the formula:
m=y2−y1x2−x1
Substituting the coordinates:
m=2−53−(−4)=−37
Step 2: Use the point-slope form to find the equation of the line.
Using point P(-4, 5) and the slope we found:
y−y1=m(x−x1)
Substituting the values:
y−5=−37(x+4)
Now, simplify this equation:
y−5=−37x−127
y=−37x+5−127
Convert 5 to a fraction:
5=357
So,
y=−37x+357−127
y=−37x+237
Step 3: Find the y-intercept (point R).
To find where the line intersects the y-axis, set x=0:
y=−37(0)+237
Thus, R(0,237).
Step 4: Calculate the distances PR and RQ.
- Distance PR:
Using the distance formula:
PR=√(x2−x1)2+(y2−y1)2
Where P(−4,5) and R(0,237):
PR=√(0−(−4))2+(237−5)2
Convert 5 to a fraction:
5=357
So,
PR=√(4)2+(237−357)2
PR=√16+(−127)2
PR=√16+14449
Convert 16 to a fraction:
16=78449
So,
PR=√784+14449=√92849=√9287=4√587
- Distance RQ:
Using the distance formula:
Where Q(3,2) and R(0,237):
RQ=√(0−3)2+(237−2)2
Convert 2 to a fraction:
2=147
So,
RQ=√(−3)2+(237−147)2
RQ=√9+(97)2
RQ=√9+8149
Convert 9 to a fraction:
9=44149
So,
RQ=√441+8149=√52249=√5227=3√587
Step 5: Find the ratio PR : RQ.
Now, we can find the ratio:
Ratio PR:RQ=PRRQ=4√5873√587=43
Thus, the ratio PR : RQ is 4:3.
---
The coordinates of points P and Q are P(-4, 5) and Q(3, 2).
m=y2−y1x2−x1
Substituting the coordinates:
m=2−53−(−4)=−37
Using point P(-4, 5) and the slope we found:
y−y1=m(x−x1)
Substituting the values:
y−5=−37(x+4)
Now, simplify this equation:
y−5=−37x−127
y=−37x+5−127
Convert 5 to a fraction:
5=357
So,
y=−37x+357−127
y=−37x+237
To find where the line intersects the y-axis, set x=0:
y=−37(0)+237
Thus, R(0,237).
- Distance PR:
Using the distance formula:
PR=√(x2−x1)2+(y2−y1)2
Where P(−4,5) and R(0,237):
PR=√(0−(−4))2+(237−5)2
Convert 5 to a fraction:
5=357
So,
PR=√(4)2+(237−357)2
PR=√16+(−127)2
PR=√16+14449
Convert 16 to a fraction:
16=78449
So,
PR=√784+14449=√92849=√9287=4√587
Using the distance formula:
Where Q(3,2) and R(0,237):
RQ=√(0−3)2+(237−2)2
Convert 2 to a fraction:
2=147
So,
RQ=√(−3)2+(237−147)2
RQ=√9+(97)2
RQ=√9+8149
Convert 9 to a fraction:
9=44149
So,
RQ=√441+8149=√52249=√5227=3√587
Now, we can find the ratio:
Ratio PR:RQ=PRRQ=4√5873√587=43
Topper's Solved these Questions
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - EXERCISE 13 (B)
20 Videos
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - EXERCISE 13 (C)
28 Videos
- SAMPLE PAPER 5 (MATHEMATICS)BOOK - ICSECHAPTER - SAMPLE PAPER 5 (MATHEMATICS)EXERCISE - SECTION C
8 Videos
- SHARES AND DIVIDENDSBOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )
20 Videos
Similar Questions
The line joining P(-4, 5) and Q(3, 2) intersects the y-axis at point R. PM and QN are perpendiculars from P and Q on the x-axis. Find:
the area of the quadrilateral PMNQ.
View SolutionThe line joining P(-4, 5) and Q(3, 2) intersects the y-axis at point R. PM and QN are perpendiculars from P and Q on the x-axis. Find:
the co-ordinates of R.
View SolutionThe line through P(5, 3) intersects y-axis at Q.

Find the co-ordinates of Q.
View SolutionThe line through P(5, 3) intersects y-axis at Q.
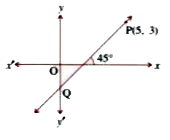
Write the slope of the line.
View SolutionUse a graph paper for this question . (Take two divisions = 1 unit on both the axes.)
Plot the points P (3,2) and Q(-3,-2) . From P and Q , draw perpendiculars PM and QN on the x - axis.
Write the co - ordinates of points M and N.
View SolutionThe line through P(5, 3) intersects y-axis at Q.

Write the equation of the line.
View SolutionUse a graph paper for this question . (Take two divisions = 1 unit on both the axes.)
Plot the points P (3,2) and Q(-3,-2) . From P and Q , draw perpendiculars PM and QN on the x - axis.
Assign the special name to geometrical figure PMQN and find its area.
View SolutionUse a graph paper for this question . (Take two divisions = 1 unit on both the axes.)
Plot the points P (3,2) and (-3,-2) . From P and Q , draw perpendiculars PM and QN on the a - axis.
Write the co-ordinates of the point to which M is mapped on reflection in :
y - axis.
View SolutionUse a graph paper for this question . (Take two divisions = 1 unit on both the axes.)
Plot the points P (3,2) and Q(-3,-2) . From P and Q , draw perpendiculars PM and QN on the x - axis.
Name the image of P on reflection in the origin.
View SolutionUse a graph paper for this question . (Take two divisions = 1 unit on both the axes.)
Plot the points P (3,2) and (-3,-2) . From P and Q , draw perpendiculars PM and QN on the a - axis.
Write the co-ordinates of the point to which M is mapped on reflection in :
x - axis.
View Solution
