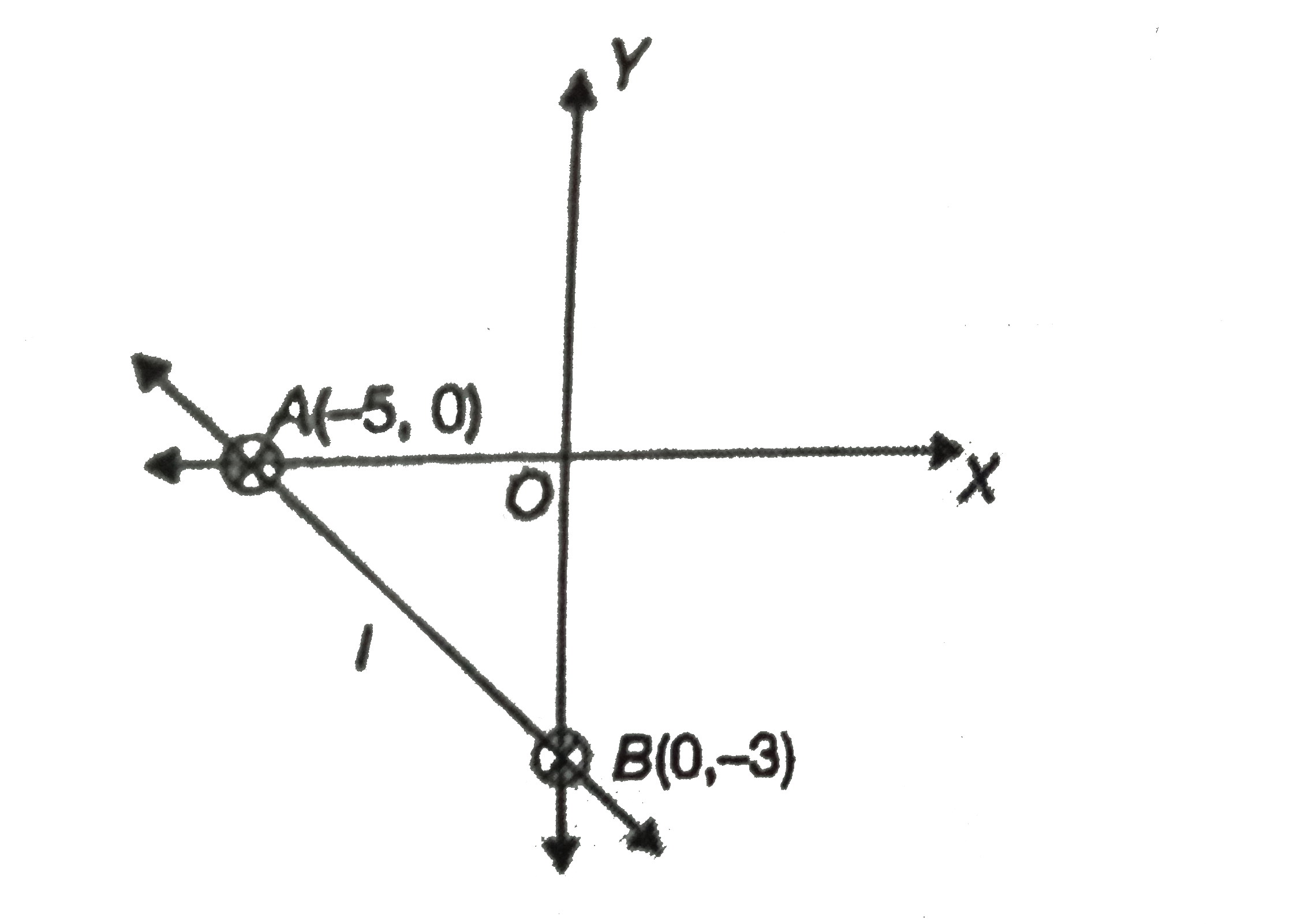
The line l in Fig14.14 meets X-axis at A(-5,0) and Y-axis at B(0,-3).
Hence , x-intercept = -5 and y-intercept = -3 .
Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Very short Answer Question
30 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Short Answer Type Questions
15 Videos
- BANKING AND COMPUTINGBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING AND COMPUTINGEXERCISE - Level 3
6 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - CONCEPT APPLICATION
61 Videos
Similar Questions
A line intersects x-axis at A(7,0) and y-axis at B(0,-5). A variable line PQ which is perpendicular to AB intersects x -axis at P and y -axis at Q. If AQ and BP intersect at r then locus of R is ………
View SolutionFor every interger n, a line Ln is drawn through the point Pn(n,n+1) perpendicular to the line x−y+1=0 meeting x-axis at An and y-axis at Bn. If O is the origin then 10∑n=0(OAn+OBn) is equal to
View Solution
Knowledge Check
A straight line through the point (1,1) meets the X-axis at A and Y-axis at B. The locus of the mid-point of AB is
A2xy+x+y=0Bx+y-2y=0Cx+y+2=0Dx+y-2=0The line 3x + 4y - 24 = 0 intersects the X - axis at A and Y-axis at B . Then the Circumcentre of the ΔOAB , where O is the origin is
A(2 , 3)B(3 , 3)C(4 ,3 )DNone of theseA line cuts the X-axis at A (5,0) and the Y-axis at B(0,−3). A variable line PQ is drawn pependicular to AB cutting the X-axis at P and the Y-axis at A. If AQ and BP meet at R, then the locus of R is
Ax2+y2−5x+3y=0Bx2+y2+5x+3y=0Cx2+y2+5x−3y=0Dx2+y2−5x−3y=0
The line 3x+2y=24 meets x - axis at B and the y -axis at A. The perpendicular bisector of AB meets the line through (0, -1) parallel to x -axis at C, then the area of the triangle ABC is_____
View SolutionThe line 3x−2y=24 meets x-axis at A and y-axis at B. The perpendicular bisector of AB meets the line through (0,−1) and parallel to x-axis at C. Then C is: (A) (−72,−1) (B) (−152,−1) (C) (−112,−1) (D) (−132,−1)
View SolutionThe line 2x+3y=12 meets the x-axis at A and y-axis at B. The line through (5,5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
View SolutionThe line 3x+2y=24 meets the y-axis at A and the x-axis at B. The perpendicular bisector of AB meets the line through (0,−1) parallel to the x-axis at C. If the area of triangle ABC is A , then the value of A13 is________
View SolutionA line cuts the x-axis at A(7,0) and the y-axis at B(0,−5) A variable line PQ is drawn perpendicular to AB cutting the x-axis in P and the y-axis in Q. If AQ and BP intersect at R, find the locus of R
View Solution
