Question

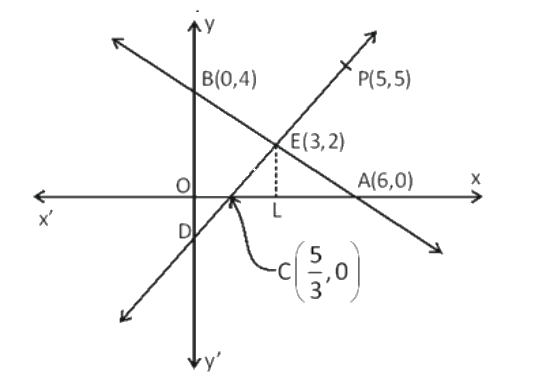
The line $2x+3y=12$
meets the x-axis at A and y-axis at B. The line through (5,5)
perpendicular to AB meets the x-axis and the line AB at C and E respectively.
If O is the origin of coordinates, find the area of figure OCEB.

Explanation

To solve the problem, we will follow these steps:

Step 1: Find the coordinates of points A and B
The line given is \(2x + 3y = 12\).

Finding point A (where the line meets the x-axis):
To find the x-intercept (point A), we set \(y = 0\):
\( 2x + 3(0) = 12 \implies 2x = 12 \implies x = 6 \)
Thus, the coordinates of point A are \((6, 0)\).

Finding point B (where the line meets the y-axis):
To find the y-intercept (point B), we set \(x = 0\):
\( 2(0) + 3y = 12 \implies 3y = 12 \implies y = 4 \)
Thus, the coordinates of point B are \((0, 4)\).

Step 2: Find the slope of line AB
The slope \(m\) of line AB can be calculated using the coordinates of points A and B:
\( m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{4 - 0}{0 - 6} = \frac{4}{-6} = -\frac{2}{3} \)

Step 3: Find the slope of the perpendicular line
The slope of the line perpendicular to AB is the negative reciprocal of the slope of AB:
\( m_{perpendicular} = -\frac{1}{m} = \frac{3}{2} \)

Step 4: Find the equation of the line through (5, 5) with the perpendicular slope
Using the point-slope form of the equation of a line:
\( y - y_1 = m(x - x_1) \)
Substituting \(m = \frac{3}{2}\) and the point \((5, 5)\):
\( y - 5 = \frac{3}{2}(x - 5) \)
Expanding this:
\( y - 5 = \frac{3}{2}x - \frac{15}{2} \)
\( y = \frac{3}{2}x - \frac{15}{2} + 5 \)
\( y = \frac{3}{2}x - \frac{15}{2} + \frac{10}{2} \)
\( y = \frac{3}{2}x - \frac{5}{2} \)

Step 5: Find the coordinates of point C (intersection with x-axis)
To find point C, set \(y = 0\):
\( 0 = \frac{3}{2}x - \frac{5}{2} \)
\( \frac{3}{2}x = \frac{5}{2} \implies x = \frac{5}{3} \)
Thus, the coordinates of point C are \(\left(\frac{5}{3}, 0\right)\).

Step 6: Find the equation of line AB
The equation of line AB can be expressed in standard form:
Using the coordinates of A and B:
\( \frac{x}{6} + \frac{y}{4} = 1 \)
Multiplying through by 12 to eliminate the fractions:
\( 2x + 3y = 12 \)

Step 7: Find the coordinates of point E (intersection of the two lines)
We need to solve the equations:
1. \(3x - 2y = 5\) (line through (5, 5))
2. \(2x + 3y = 12\) (line AB)

To solve these equations, we can multiply the first by 3:
\( 9x - 6y = 15 \)
And multiply the second by 2:
\( 4x + 6y = 24 \)
Now, adding these two equations:
\( 9x - 6y + 4x + 6y = 15 + 24 \)
\( 13x = 39 \implies x = 3 \)
Substituting \(x = 3\) back into the first equation to find \(y\):
\( 3(3) - 2y = 5 \implies 9 - 2y = 5 \implies -2y = -4 \implies y = 2 \)
Thus, the coordinates of point E are \((3, 2)\).

Step 8: Find the area of figure OCEB
The vertices of the quadrilateral OCEB are:
- O(0, 0)
- C\(\left(\frac{5}{3}, 0\right)\)
- E(3, 2)
- B(0, 4)

To find the area of quadrilateral OCEB, we can divide it into two triangles: OCE and OBE.

Area of triangle OCE:
Using the formula for the area of a triangle given vertices \((x_1, y_1)\), \((x_2, y_2)\), \((x_3, y_3)\):
\( \text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \)
Substituting O(0, 0), C\(\left(\frac{5}{3}, 0\right)\), E(3, 2):
\( \text{Area}_{OCE} = \frac{1}{2} \left| 0(0 - 2) + \frac{5}{3}(2 - 0) + 3(0 - 0) \right| = \frac{1}{2} \left| \frac{10}{3} \right| = \frac{5}{3} \)

Area of triangle OBE:
Using the same formula for vertices O(0, 0), B(0, 4), E(3, 2):
\( \text{Area}_{OBE} = \frac{1}{2} \left| 0(4 - 2) + 0(2 - 0) + 3(0 - 4) \right| = \frac{1}{2} \left| -12 \right| = 6 \)

Total Area of OCEB:
\( \text{Area}_{OCEB} = \text{Area}_{OCE} + \text{Area}_{OBE} = \frac{5}{3} + 6 = \frac{5}{3} + \frac{18}{3} = \frac{23}{3} \)

Final Answer:
The area of figure OCEB is \(\frac{23}{3}\).

---